RoboCup 2015 - Pyro Team : Différence entre versions
(→Jour 2 :) |
|||
| (131 révisions intermédiaires par 3 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| + | <include nopre noesc src="/home/pedago/pimasc/include/video-OpenGermanII-iframe.html" /> | ||
__TOC__ | __TOC__ | ||
<br style="clear: both;"/> | <br style="clear: both;"/> | ||
| Ligne 59 : | Ligne 60 : | ||
**D-Star Lite au lieu de A-Star | **D-Star Lite au lieu de A-Star | ||
**Filtrage des données laser | **Filtrage des données laser | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Avancement du Projet== | ==Avancement du Projet== | ||
| Ligne 78 : | Ligne 68 : | ||
===Semaine 2=== | ===Semaine 2=== | ||
| − | ==== | + | ====Etablissement du cahier des charges==== |
| − | |||
*Prise de connaissance des contraintes d'environnement | *Prise de connaissance des contraintes d'environnement | ||
*Dialogue avec l'équipe responsable de la partie [http://projets-imasc.plil.net/mediawiki/index.php?title=RoboCup_2015 Manager] | *Dialogue avec l'équipe responsable de la partie [http://projets-imasc.plil.net/mediawiki/index.php?title=RoboCup_2015 Manager] | ||
| − | Familiarisation avec l'environnement logiciel ROS | + | *Familiarisation avec l'environnement logiciel ROS |
| − | Recherches de solutions pour la localisation (SLAM) | + | *Recherches de solutions pour la localisation (SLAM) |
| − | + | *Recherche de solution pour la génération de trajectoire (algorithme A-star) | |
| − | |||
| − | ==== | + | ====Recherche d'un algorithme de recherche de chemin==== |
| − | Nous avons fait nos recherches en nous orientant sur le déplacement du Robotino afin de trouver un algorithme de | + | Nous avons fait nos recherches en nous orientant sur le déplacement du Robotino afin de trouver un algorithme de recherche de chemin, capable de trouver le chemin le plus court, puisqu'un des buts de la compétition étant la rapidité.<br> |
Plusieurs algorithmes sont donc ressortis :<br> | Plusieurs algorithmes sont donc ressortis :<br> | ||
*L'algorithme Dijkstra (On part du point de départ et on cherche le chemin le plus court vers le point d'arrivée en cherchant dans TOUTES les directions)<br> | *L'algorithme Dijkstra (On part du point de départ et on cherche le chemin le plus court vers le point d'arrivée en cherchant dans TOUTES les directions)<br> | ||
*L'algorithme A-Star (Basé sur Dijkstra, cet algo s'oriente directement vers le point d'arrivée en minimisant la distance avec celui-ci)<br> | *L'algorithme A-Star (Basé sur Dijkstra, cet algo s'oriente directement vers le point d'arrivée en minimisant la distance avec celui-ci)<br> | ||
*L'algorithme D-Star Lite (Amélioration du A-Star avec bufferisation des précédents calculs pour éviter les calculs inutiles en cas d'arrivée d'un obstacle mobile sur la trajectoire)<br> | *L'algorithme D-Star Lite (Amélioration du A-Star avec bufferisation des précédents calculs pour éviter les calculs inutiles en cas d'arrivée d'un obstacle mobile sur la trajectoire)<br> | ||
| + | |||
| + | Nous avons visualisé les différents algorithmes sur [http://qiao.github.io/PathFinding.js/visual/ PathFinding] | ||
Fonctionnement de l'algorithme A-Star :<br> | Fonctionnement de l'algorithme A-Star :<br> | ||
| Ligne 113 : | Ligne 103 : | ||
*Attention : c'est seulement lorsqu'il aura trouvé le chemin complet que le robot va se déplacer ! | *Attention : c'est seulement lorsqu'il aura trouvé le chemin complet que le robot va se déplacer ! | ||
| − | ==== | + | ====Recherche d'une solution pour la localisation==== |
| − | Pour la localisation nous allons utilisé un | + | Pour la localisation nous allons utilisé un '''''Algorithme de Localisation et Cartographie Simultanée''''' (SLAM en anglais): |
| − | [[Fichier:SLAM.png | center]] | + | [[Fichier:SLAM.png | center | thumb]] |
Explicitation des différentes parties : | Explicitation des différentes parties : | ||
| Ligne 134 : | Ligne 124 : | ||
===Semaine 3=== | ===Semaine 3=== | ||
| − | ==== | + | ====Découpage du travail à effectuer==== |
| − | + | Nous avons découper le travail de génération de map et de la correction de position de la manière suivante : | |
[[Fichier:SchémaProjetS8-1.png | 800px | center]] | [[Fichier:SchémaProjetS8-1.png | 800px | center]] | ||
| Ligne 142 : | Ligne 132 : | ||
( Nous recommandons au lecteur de se référer à la partie vocabulaire pour comprendre les termes techniques ) | ( Nous recommandons au lecteur de se référer à la partie vocabulaire pour comprendre les termes techniques ) | ||
| − | + | Chaque case du diagramme précédent correspond à un noeud ROS. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Décrivons précisément le rôle de chaque noeud : | |
| + | *'''Laser''' récupère les données brutes du laser. | ||
| + | *'''Filtrage''' permet, comme son nom l'indique, d'enlever les éventuels bruits qui affectent les données du laser. | ||
| + | *'''Reconnaissance des droites''' traite les données laser filtrées pour détecter les droites présentes (Transformée de Hough ou Ransac) | ||
| + | *'''Reconnaissance des formes''' extrapole les objets (machines) à partir des droites. | ||
| + | *'''Corrélation emplacements machines''' lie la position des machines détectées au laser et les positions envoyées par RefBoxCom pour éviter les incohérences. | ||
| + | *'''Odométrie''' récupère la position du robot par rapport au point de départ. Il renvoie une position corrigée grâce au gyroscope(Pose) et une position non corrigée par le gyroscope (Twist) | ||
| + | *'''Traitement de position''' corrige l'erreur sur le Twist avec les données du gyroscope (par dérivation). | ||
| + | *'''Fusion de Kalman''' est un algorithme qui va coupler les données de position et les données du laser afin de fournir un modèle et une position précise. C'est le noeud central du SLAM. | ||
| + | *'''Stockage machines + robot''' transforme les positions des machines et du robot en grille. Il sera couplé aux détections d'obstacles. | ||
| + | *'''Grid Map''' renvoit une map utilisée ensuite pour les déplacements et les calculs de trajectoires (A_Star) | ||
| + | *'''RefBoxCom''' stocke et renvoie la position des machines. | ||
| + | *'''Position robot''' renvoie la position exacte du robot sur la grille. | ||
| + | *'''Manager''' Noeud qui envoie la position à atteindre. | ||
| + | *'''Pathfinder''' recherche le chemin demandé par le Manager sur une grille | ||
| + | *'''Parcoureur''' exécute le chemin trouvé en fournissant les vitesses au noeud Déplacement. | ||
| + | *'''Déplacement''' (noeud robotino_local_move_server), qui donne les commandes aux moteurs à partir de la vitesse linéaire et angulaire envoyée par le Parcoureur. | ||
| − | + | ====Recherche de documentation sur ROS et l'API du Robotino==== | |
| − | [http://wiki.ros.org/fr Wiki_ROS] | + | Nous avons cherchés toutes les documentations techniques nécessaires pour la programmation de chaque noeud : [http://wiki.ros.org/fr Wiki_ROS] et [http://wiki.ros.org/robotino API_Robotino], nous permettant de mettre à jour le schéma global, notamment au niveau des types. |
| − | + | ====Etude de l'algorithme A-star précédent==== | |
| − | + | Nous nous sommes ensuite concentrés sur le noeud GridMap qui contient ''Map.cpp'' : | |
| − | + | Dans le code de l'an dernier, ce noeud générait une grille en dur. Cependant, cette solution n'est pas possible cette année car nous ne connaissons pas toutes les informations sur la piste (on connaît à peu près la position mais pas l'orientation). Il va donc falloir générer une grille en fonction du noeud précédent qui nous renverra un type ''OccupancyGrid''. | |
| − | |||
| − | |||
| − | Dans le code de l'an dernier, ce noeud | ||
| − | |||
Etant donné que ce noeud tournera en permanence, si des informations changent pendant que le robot est sur la piste (détection des nouvelles machines par exemple), le noeud ''Map.cpp'' modifiera la grille en temps réel. | Etant donné que ce noeud tournera en permanence, si des informations changent pendant que le robot est sur la piste (détection des nouvelles machines par exemple), le noeud ''Map.cpp'' modifiera la grille en temps réel. | ||
| − | |||
La grille est décomposée en case pour le A-Star : | La grille est décomposée en case pour le A-Star : | ||
| − | Si c'est une case interdite (obstacle) ont associe a la case la valeur 1, si elle est autorisée, on associe la valeur 0. | + | Si c'est une case interdite (obstacle) ont associe a la case la valeur 1, si elle est autorisée, on associe la valeur 0. On illustre le principe précédent par un exemple : |
| − | |||
| − | On illustre le principe précédent par un exemple : | ||
| − | |||
[[Fichier:Projet_S8_Creation_Map.PNG | 800px | center]] | [[Fichier:Projet_S8_Creation_Map.PNG | 800px | center]] | ||
| − | + | Cependant, le noeud "Grid Map" va nous délivrer un vecteur et non une matrice par le biais de ''OccupancyGrid.Data''.Dans notre exemple précédent, on récupère le vecteur suivant : | |
| − | Cependant, le noeud "Grid Map" va nous délivrer un vecteur et non une matrice par le biais de ''OccupancyGrid.Data'' . | ||
| − | |||
| − | Dans notre exemple précédent, on récupère le vecteur suivant : | ||
| − | |||
[[Fichier:Projet_S8_Creation_Map_2.PNG | 800px | center]] | [[Fichier:Projet_S8_Creation_Map_2.PNG | 800px | center]] | ||
| − | + | On choisit donc de transformer ce vecteur en matrice, car l'algorithme A-Star fonctionne sur un graphe, pas un vecteur. On connait la largeur (en case) de la grille grâce au type ''OccupancyGrid.info.width''. | |
| − | On choisit donc de transformer ce vecteur en matrice. On connait la largeur (en case) de la grille grâce au type ''OccupancyGrid.info.width''. | ||
Le pseudo-code pour générer la matrice à partir de ce vecteur sera le suivant : | Le pseudo-code pour générer la matrice à partir de ce vecteur sera le suivant : | ||
| Ligne 214 : | Ligne 192 : | ||
} | } | ||
} | } | ||
| + | return matrice; | ||
| + | } | ||
| + | |||
| + | ===Semaine 4=== | ||
| + | |||
| + | ====Localisation - Landmarks Extraction==== | ||
| + | |||
| + | Nous nous concentrons essentiellement sur la première partie, qui est la partie : "Landmarks Extraction" (extraction des points de repères). On travaille ici dans le repère du laser, qui est différent de celui du robot, et du global. La transposition dans le repère global se fera dans la partie "Data Association". On doit ainsi, dans l'ordre : | ||
| + | |||
| + | ☑ récupérer des données lasers via le topic /scan<br> | ||
| + | ☑ convertir les coordonnées polaires en coordonnées cartésiennes en filtrant les données aberrantes (> range_max et < range_min)<br> | ||
| + | ☑ implémenter l'algorithme [http://fr.wikipedia.org/wiki/RANSAC RANSAC] (Random SAmple Consensus) de détection de droites :<br> | ||
| + | ☑ détecter la "meilleure" droite à partir des points en sélectionnant aléatoirement des combinaisons de points<br> | ||
| + | ☑ stocker le meilleur modèle (angle + tableau de points)<br> | ||
| + | ☑ recommencer tant qu'il reste assez de points à traiter (5)<br> | ||
| + | ☑ extraire les segments à partir des modèles trouvés et des points<br> | ||
| + | ☑ extraire les points extrèmes<br> | ||
| + | ☑ calculer la taille du segment<br> | ||
| + | ☑ chercher des angles droits, des segments de 35 ou 70 cm (largeur et longueur d'une machine)<br> | ||
| + | ☑ extrapoler les positions des machines dans le repère du laser<br> | ||
| + | ☑ définir le barycentre de la machine ainsi que son angle<br> | ||
| + | ☐ stocker ces positions<br> | ||
| + | |||
| + | ====Pathfinder==== | ||
| + | |||
| + | Nous avons aussi pris du temps avec '''Valentin VERGEZ''', qui a développé, l'an dernier, les codes pour le déplacement du Robotino et le calcul de trajectoire | ||
| + | |||
| + | Nous avons éclairci quelques points sur cette partie du projet : | ||
| + | *Les commentaires sur l'utilité de chaque fonction ont été rajoutés. | ||
| + | *Le "code mort" a été nettoyé ainsi que les parties inutiles. | ||
| + | *Nous devons trouver un moyen de tester cette partie du code seule. (A priori graphiquement). | ||
| + | |||
| + | Etant donné l'arrivée d'un nouvel ordinateur au sein de l'équipe, nous en avons profités pour installer les logiciels qui nous permettrons de faire tourner les noeuds codés sur les Robotino : | ||
| + | |||
| + | *Installation d'Ubuntu 12.04 ( c'est cette version qui permet de faire tourner ROS Hydro) | ||
| + | |||
| + | *Installation de ROS Hydro (ensemble d'outils informatiques open source permettant de développer des logiciels pour la robotique.) | ||
| + | |||
| + | *Installation des paquets nécessaires (catkin, Desktop Install, ROS-Base, Individual Package) | ||
| + | |||
| + | *Installation de GIT (outil de bas niveau permettant de gérer l'évolution du contenu d'une arborescence) | ||
| + | |||
| + | *Vérification que toutes les fonctionnalités de ROS Hydro étaient présentes ( [http://wiki.ros.org/ROS/Tutorials Tutoriel]) | ||
| + | |||
| + | La récupération du code complet de l'année dernière et une solution a été trouvée afin de tester le code de génération de trajectoire A-star: | ||
| + | |||
| + | *Pour visualiser une Map ainsi qu'un Path (chemin), on peut utiliser l'outils [http://wiki.ros.org/rviz RVIZ]. | ||
| + | *Dans RVIZ, on peut ajouter un Path (topic /path), ainsi qu'ajouter une Map (/grid): Ceci correspond exactement à ce que nous souhaitons visualiser pour la partie calcul de trajectoire. | ||
| + | *Pour publier une Map fictive, on executera le script fakeGrid.sh | ||
| + | *Pour générer un chemin, on lancera le pathfinder (rosruns rbqt_pathfinder server : notre code) et on effectuera une requête avec le script pathReq.sh. | ||
| + | |||
| + | Si tout se passe correctement, le chemin devrait s'afficher en <span style="color: #00FF00;"> vert </span> sur la map. | ||
| + | |||
| + | Nous avons aussi du communiquer notre avancement aux autres parties de l'équipe. Le schéma général ainsi qu'un outil permettant d'expliquer les différents algorithmes de recherche de trajectoire optimale nous ont aidé à leur communiquer nos objectifs et les processus choisis. | ||
| + | |||
| + | L'algorithme A-Star que nous allons utiliser donne le résultat final suivant (utilisation du site [http://qiao.github.io/PathFinding.js/visual/ PathFinding] ): | ||
| + | |||
| + | [[Fichier:Projet S8 A STAR E.PNG | center | thumb ]] | ||
| + | |||
| + | * <span style="color: #FFFF00;"> le chemin optimal calculé par A-Star </span> | ||
| + | * <span style="color: #008000;"> le point de départ</span> | ||
| + | * <span style="color: #FF0000;"> le point d'arrivée</span> | ||
| + | * <span style="color: #808080;"> les points interdits (obstacle)</span> | ||
| + | * <span style="color: #00FFFF;"> les points que l'algorithme a déjà calculé</span> | ||
| + | * <span style="color: #00FF00;"> les points que l'algorithme aurait calculé à la prochaine itération</span> | ||
| + | |||
| + | ====Localisation - Landmarks extraction - filtrage==== | ||
| + | |||
| + | Dans cette partie, nous avons commencé à définir une classe laserScan qui contient la fonction polarToCart, elle convertit les données laser (tableau de ranges) en liste de points (x,y) : | ||
| + | |||
| + | void laserScan::PolarToCart (){ | ||
| + | Point p; | ||
| + | for (int i=0; i<m_ranges.size(); i++){ | ||
| + | if((m_ranges[i]>getRangeMin()) && (m_ranges[i]<getRangeMax())){ | ||
| + | p.setX(m_ranges[i]*cos(getAngleMin() + i*getAngleInc())); | ||
| + | p.setY(m_ranges[i]*sin(getAngleMin() + i*getAngleInc())); | ||
| + | m_points.push_back(p); | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | ====Localisation - Landmarks extraction - reconnaissance de droite==== | ||
| + | |||
| + | Dans cette partie, nous avons déterminé quel algorithme nous allons utiliser : [http://fr.wikipedia.org/wiki/RANSAC#L.27algorithme RANSAC]. L'algorithme de RANSAC trouve la meilleure droite dans un nuage de points. On itère plusieurs fois cet algorithme afin de trouver l'ensemble de toutes les droites du scan laser. On a donc en sortie une liste des droites composants le nuage de points initial. | ||
| + | |||
| + | Entrée : listOfPoints -> liste de points initiale | ||
| + | Sortie : meilleur_modèle -> les paramètres de la droite qui correspondent le mieux aux points | ||
| + | -> tableau de points à partir desquels la droite a été estimée | ||
| + | -> erreur du modèle de droite par rapport aux points | ||
| + | <span style="color: #000080;"> | ||
| + | tant que la liste contient assez de points | ||
| + | itérateur := 0 | ||
| + | meilleur_modèle := aucun | ||
| + | tant que itérateur < k (fixé par une loi de probabilité) | ||
| + | <span style="color: #008000;">on choisit deux points au hasard dans la liste</span> | ||
| + | <span style="color: #00FFFF;">on fabrique un modèle_possible à partir de ces deux points</span> | ||
| + | <span style="color: #FF0000;">Pour chaque point de la liste qui ne sont pas dans le modele_possible | ||
| + | si le point s'ajuste au modele_possible avec une erreur inférieure à t | ||
| + | Ajouter ce point au modele</span> | ||
| + | <span style="color: #00FF00;">si le nombre de points dans le modele est suffisant pour valider l'existence du modele | ||
| + | erreur := coefficient de corrélation de la régression linéaire de ensemble_points</span> | ||
| + | <span style="color: #808080;">si erreur < erreur du meilleur_modele | ||
| + | meilleur_modèle := modèle_possible</span> | ||
| + | |||
| + | stocker meilleur_modèle dans liste de modèles | ||
| + | retirer meilleur_ensemble_points de la liste des points initiale | ||
| + | recommencer avec la liste modifiée | ||
| + | |||
| + | ===Semaine 5=== | ||
| + | |||
| + | ====Localisation - Landmarks Extraction - reconnaissance de droite==== | ||
| + | |||
| + | Nous avons adapté l'algorithme précédent afin de mieux correspondre aux structures que nous avons créées : | ||
| + | *Modele | ||
| + | **Liste de points | ||
| + | **Liste d'indices | ||
| + | **Corrélation | ||
| + | **Droite | ||
| + | ***Point | ||
| + | ***Angle | ||
| + | **Segment | ||
| + | ***Point "min" | ||
| + | ***Point "max" | ||
| + | ***Angle | ||
| + | ***Taille | ||
| + | |||
| + | Nous avons aussi codé toutes les fonctions nécessaires dans l'algorithme de Ransac, dont celle permettant la correction de l'approximation de droite par régression linéaire des points correspondants à un modèle trouvé (''linReg()'') qui nous a donné matière à réflexion. Aussi, notre première idée qui était de travailler avec des ''std::vector'' a du changer puisque l'aspect récursif de l'algorithme que nous allons utiliser nécessite de multiples suppressions sur les données à entrer dans l'algorithme de Ransac. On travaille donc maintenant avec des ''std::list''. | ||
| + | |||
| + | Tous nos codes sont disponibles sur la branche [https://github.com/PyroTeam/robocup-pkg/tree/feature/navigation/SLAM/navigation/localisation/src feature/navigation/SLAM du GIT de l'équipe PyroTeam]. | ||
| + | |||
| + | ===Semaine de vacances de février=== | ||
| + | |||
| + | ====Localisation - Landmarks Extraction - reconnaissance de droite==== | ||
| + | |||
| + | Nous devons réaliser un noeud permettant de valider notre algorithme, c'est-à-dire implémenter sous ROS notre code C++ afin de tester, soit directement sur le robot, soit avec des [http://wiki.ros.org/Bags bagfiles]. Cette étape est très importante pour pouvoir passer à la suite : extrapoler les droites trouvées en segments puis en objets. | ||
| + | |||
| + | Notre programme consistant à reconnaître les droites à partir du scan laser est fonctionnel et a été testé à partir du scan laser suivant : | ||
| + | |||
| + | [[Fichier:ScanLaser.png | center | thumb]] | ||
| + | |||
| + | Processus de validation : | ||
| + | |||
| + | *Lancer le programme ''rosrun localisation test_polar_to_cart'' | ||
| + | |||
| + | résultat : on trouve 5 droites | ||
| + | |||
| + | m = -0.0229637 p = -0.24079 | ||
| + | nb de points dans la droite : 246 | ||
| + | coeff de correlation : 0.812376 | ||
| + | |||
| + | m = -0.0315132 p = 3.7506 | ||
| + | nb de points dans la droite : 102 | ||
| + | coeff de correlation : 0.928089 | ||
| + | |||
| + | m = 32.9243 p = -139.943 | ||
| + | nb de points dans la droite : 77 | ||
| + | coeff de correlation : 0.914475 | ||
| + | |||
| + | m = 7.04634 p = -15.42 | ||
| + | nb de points dans la droite : 32 | ||
| + | coeff de correlation : 0.970724 | ||
| + | |||
| + | m = 0.253029 p = 1.32235 | ||
| + | nb de points dans la droite : 28 | ||
| + | coeff de correlation : 0.979578 | ||
| + | |||
| + | ce qui correspond à l'image suivante : | ||
| + | |||
| + | [[Fichier:DroitesTrouvées.png | center | thumb]] | ||
| + | |||
| + | On voit que la recherche de droite marche bien, mais peut être améliorée en ajoutant des conditions de proximité des points correspondants à une seule droite, pour éviter le phénomène que l'on voit au milieu. Le résultat après avoir ajouté cette condition et en ayant affiné au maximum les paramètres, au dépend d'un temps de calcul beaucoup plus élevé (9,416 secondes au lieu de 0,536 s) : | ||
| + | |||
| + | [[Fichier:DroitesTrouvées2.png | center | thumb]] | ||
| + | |||
| + | Les impératifs de la compétition nous imposant une certaine rapidité pour se localiser et détecter les machines, nous retiendrons la solution la plus rapide et nous séparerons les droites en segment après leur détection. | ||
| + | |||
| + | Pour valider l'algorithme de régression linéaire nous avons : | ||
| + | *Récupéré tous les points correspondants à chaque droite | ||
| + | *Rentré ces points sur Excel | ||
| + | *Fait une courbe de tendance | ||
| + | *Affiché l'équation de droite et le coefficient de corrélation | ||
| + | *Comparé avec ce qu'a trouvé notre programme | ||
| + | *Conclu que notre programme était bon | ||
| + | |||
| + | ===Semaine 6=== | ||
| + | |||
| + | ====Localisation - Landmarks Extraction - reconnaissance de machines==== | ||
| + | |||
| + | Les objectifs de cette semaine : | ||
| + | |||
| + | *à partir de la liste de droites, extraire les segments | ||
| + | *extrapoler les positions machines à partir d'un segment complet (35 ou 70 cm) | ||
| + | *réaliser une interface graphique pour visualiser les segments trouvés en temps réel | ||
| + | *regarder ce qu'on doit rentrer dans l' '''Extended Kalman Filter''' au niveau du format des positions machines et de l'odométrie pour pouvoir réaliser le '''Data Association''' de façon cohérente avec la suite. | ||
| + | |||
| + | L'extraction de segment à partir des 5 droite précédemment trouvées nous donne 7 segments: | ||
| + | |||
| + | Segment 1<br> | ||
| + | Min(-1.04033e-08, -0.238) | ||
| + | Max(4.24699, -0.26092) | ||
| + | taille : 4.24705 | ||
| + | angle : -0.309205 | ||
| + | |||
| + | |||
| + | Segment 2<br> | ||
| + | Min(-1.64267e-07, 3.758) | ||
| + | Max(3.4172, 3.63358) | ||
| + | taille : 3.41946 | ||
| + | angle : -2.08521 | ||
| + | |||
| + | |||
| + | Segment 3<br> | ||
| + | Min(4.24452, -0.234635) | ||
| + | Max(4.33124, 2.18017) | ||
| + | taille : 2.41636 | ||
| + | angle : 87.9432 | ||
| + | |||
| + | |||
| + | Segment 4<br> | ||
| + | Min(2.30055, 0.871242) | ||
| + | Max(2.32511, 0.736592) | ||
| + | taille : 0.136872 | ||
| + | angle : -79.6622 | ||
| + | |||
| + | |||
| + | Segment 5<br> | ||
| + | Min(2.50359, 2.18655) | ||
| + | Max(2.53413, 2.56542) | ||
| + | taille : 0.380104 | ||
| + | angle : 85.3914 | ||
| + | |||
| + | |||
| + | Segment 6<br> | ||
| + | Min(2.73122, 2.05171) | ||
| + | Max(3.049, 2.03728) | ||
| + | taille : 0.318107 | ||
| + | angle : -2.5999 | ||
| + | |||
| + | |||
| + | Segment 7<br> | ||
| + | Min(1.14156, 1.64221) | ||
| + | Max(1.39648, 1.61891) | ||
| + | taille : 0.255984 | ||
| + | angle : -5.22068 | ||
| + | |||
| + | [[Fichier:SegmentsTrouvés.png | center | thumb]] | ||
| + | |||
| + | Tout cela en 0,540s ! | ||
| + | |||
| + | A partir de la liste de segments précédente, on extrait une liste de machine à partir des segments de 35 ou 70 cm, qui sont les tailles des machines. Comme le scan que nous utilisons pour le moment n'est pas un scan avec une vraie machine, mais disposant quand même de 2 segments d'à peu près 35 cm, nous utilisons ces deux segments comme ''petit côté'' de la machine. On trouve ainsi deux machines : | ||
| + | |||
| + | Machine 1 | ||
| + | centre en (2.53292, 2.20155) | ||
| + | orientation : 175.391° | ||
| + | |||
| + | Machine 2 | ||
| + | centre en (3.06493, 2.05243) | ||
| + | orientation : 87.4001° | ||
| + | |||
| + | |||
| + | Une amélioration de l'algorithme a été faite pour la détection de machine. En effet, dans le cas où on détectait un petit et un grand côté de machine, on trouvait deux machines avec des centres à peu près au même endroit. Maintenant, on fusionne ces données en créant un point milieu entre les deux données, et on prend l'orientation du grand côté. | ||
| + | |||
| + | On a commencé à faire des tests sur ROS directement avec un noeud factice qui publie un scan laser à une fréquence de 10Hz, ce qui est la fréquence réelle du laser Hokuyo. La détection se fait assez rapidement et de façon précise. Des tests sur le robot sont prévus en début de semaine 7 avec les vraies machines. | ||
| + | |||
| + | ===Semaine 7=== | ||
| + | |||
| + | ====Localisation - Data Association==== | ||
| + | |||
| + | L'objectif principal de cette semaine est de coder le noeud '''Data Association''' qui liera la position donnée par l'odométrie (mesure relative de la position par rapport à un point de départ à peu près connu) avec les machines trouvées dans le champ du laser. | ||
| + | |||
| + | Il faudra aussi corriger l'odométrie donné par le nœud ''robotino_odometry_node'', qui donne l'odométrie (mesure de la position et de la vitesse du robot). Le problème est que nous utilisons un gyroscope externe, car le gyroscope de base est de très basse qualité. Or, si le nœud corrige parfaitement la position, il ne corrige pas du tout la vitesse angulaire ! Nous devons donc réaliser un nœud qui le fera pour nous. | ||
| + | |||
| + | D'après la dernière version du sujet 2015, l'aire de jeu de 6 x 12 m est séparée en zones de 1,5 x 2 m de large, dans lesquelles se situent une seule machine. Chaque équipe a 6 machines dont la zone est connue, donnée par la Referee Box. Le but du nœud ROS de ''Data Association'' sera de transposer les positions machines dans le repère global de la piste, ainsi le Manager pour savoir devant quelle machine le robot est, et connaître sa position et son orientation. | ||
| + | |||
| + | La piste sera donc comme cela : | ||
| + | |||
| + | [[Fichier:Piste.PNG | center | thumb]] | ||
| + | |||
| + | La correction d'odométrie a fait apparaître une erreur de mesure d'environ 1,7°/s sur la vitesse angulaire, à faible vitesse. Pour de la Localisation et Cartographie Simultanée, c'est assez important. Ça justifie donc la nécessité de faire cet ajustement. | ||
| + | |||
| + | Pour la suite, il a été décidé de fusionner les nœuds '''Data Association''' et '''Extended Kalman Filter''' puisque l'association de données n'étant au final qu'un changement de repère, la structure de nœud ROS n'est pas adaptée. | ||
| + | |||
| + | Nous avons trouvé un [https://github.com/yangyimeng/machine-learning/blob/master/slam/EKF/SLAM%20course.pdf PDF] expliquant l'algorithme de SLAM. Grâce à celui ci nous avons déterminer les éléments à rentrer dans le noeud, ainsi que les différentes opérations incluses dans ce filtre. Pour les calculs matriciels, nous allons probablement utiliser la librairie EIGEN pour travailler sur des [http://eigen.tuxfamily.org/dox/classEigen_1_1Matrix.html matrices] de façon optimisée. La prochaine étape sera de "typer" nos informations (position robot + machine + murs) pour pouvoir les intégrer facilement au filtre. Nous avons aussi décidé d'inclure les murs comme ''landmark'' dans la matrice de covariance du vecteur d'état. | ||
| + | |||
| + | Il a été décidé de faire une association de données avant la détection de machines, pour distinguer les pans de murs directement afin de stocker ces informations directement à la source. On pourra éventuellement détecter les coins intérieurs de la piste pour plus de précision dans le recalage. Pour le reste, rien ne change. | ||
| + | |||
| + | |||
| + | ===Semaine 8=== | ||
| + | |||
| + | ====Localisation - Landmarks Extraction - vidéo==== | ||
| + | |||
| + | Pour visualiser les résultats de la détection des machines nous avons utiliser l'interface graphique disponible avec ROS, RVIZ. Nous visualisons alors le scan laser (points blancs), le résultat de la détection de segments (en rouge) et les positions des machines trouvées (en vert). Un premier test a été fait sur le scan originel, celui sur lequel nous avons travaillé depuis le début. | ||
| + | |||
| + | [https://www.youtube.com/watch?v=XSn4s1y-XT0 Visualisation des machines] | ||
| + | |||
| + | On rencontre un problème quand le robot est exactement parallèle ou perpendiculaire à un mur. Après vérification dans le programme, il s'avère que la détection ne fonctionne pas pour ces cas. Ce bug est maintenant corrigé : | ||
| + | |||
| + | [https://www.youtube.com/watch?v=rKeqewpuLoQ Correction du bug] | ||
| + | ====Localisation - Data Association==== | ||
| + | |||
| + | La première étape consiste juste à faire un changement de repère, d'abord du repère laser vers le repère robot, puisque le laser sera placé en avant du robot, puis du repère robot au repère global, comme ci dessous : | ||
| + | |||
| + | [[Fichier:Chgt_Repère.png |center | thumb]] | ||
| + | |||
| + | la matrice correspondant au changement (laser -> robot) est la suivante : | ||
| + | |||
| + | 0 -1 0 | ||
| + | 1 0 0.2 | ||
| + | 0 0 1 | ||
| + | |||
| + | la matrice 2x2 en haut à gauche correspond à la rotation de 90°, et le vecteur (0, 0.2) correspond à la translation. | ||
| + | |||
| + | Celle du changement (robot -> global) avec alpha angle mesuré par le gyroscope depuis la position initiale (angle 0) : | ||
| + | |||
| + | cos(alpha) -sin(alpha) posInit.x | ||
| + | sin(alpha) cos(alpha) posInit.y | ||
| + | 0 0 1 | ||
| + | |||
| + | l'étape suivante est de vérifier si les machines vues par le laser sont bien des machines, c'est-à-dire si les positions mesurées à partir des données lasers correspond aux zones occupées par des machines envoyées par la Referee Box. | ||
| + | |||
| + | |||
| + | ====Grid Map==== | ||
| + | |||
| + | L'autre objectif de cette semaine a été de coder le noeud qui génère la map. La map est générée sous forme d'OccupancyGrid. Ce type est constitué d'un seul vecteur dont la première case correspond à la case en bas à gauche de la map. D'autres paramètres sont réglable comme l'origine et la taille. | ||
| + | |||
| + | Pour la taille on choisit de diviser la map en case de 10 cm et l'origine choisie est le x du centre de la map et en y l'abscisse du premier mur (voir la map ci-dessous). Afin d'expliquer comment est constituée cette map, prenons le code et analysons les différentes fonctions ainsi que le main : | ||
| + | |||
| + | Ce vecteur de Pose2D (x, y et theta (angle de la machine)) va permettre d'enregistrer la position des machines, c'est une variable global qui sera mise à jour avec le Callback : | ||
| + | |||
| + | std::vector<geometry_msgs::Pose2D> tab; | ||
| + | |||
| + | *Récupération des machines envoyées par le noeud du SLAM (sur le topic /landmarks): | ||
| + | |||
| + | void Poses_Machine_Callback(const deplacement_msg::LandmarksConstPtr &machines) | ||
| + | { | ||
| + | tab=machines->landmarks; | ||
| + | for (int i=0; i<tab.size(); i++) | ||
| + | { | ||
| + | tab[i].x = tab[i].x*1000; | ||
| + | tab[i].y = tab[i].y*1000; | ||
| + | } | ||
| + | |||
| + | } | ||
| + | |||
| + | *Création d'une map vide de taille 14m sur 8m. Chaque case est initialisée à une valeur nulle, on remplit également les autres paramètres de OccupancyGrid: | ||
| + | (On rappelle que la technique utilisée est un vecteur qui représente chaque case auxquelles il associe une probabilité 100 c'est un point interdit et 0 quand c'est un point sans danger pour le passage du robot) | ||
| + | |||
| + | void Create_Empty_Map(nav_msgs::OccupancyGrid &Map) | ||
| + | { | ||
| + | Map.info.origin.position.x=-7000; | ||
| + | Map.info.origin.position.y=-1000; | ||
| + | Map.info.origin.position.z=0; | ||
| + | Map.info.origin.orientation.x=0; | ||
| + | Map.info.origin.orientation.y=0; | ||
| + | Map.info.origin.orientation.z=0; | ||
| + | Map.info.origin.orientation.w=1; | ||
| + | Map.info.map_load_time=ros::Time::now(); | ||
| + | Map.info.resolution=100; | ||
| + | Map.info.width=140; | ||
| + | Map.info.height=80; | ||
| + | Map.data.assign(Map.info.width*Map.info.height, 0); //map vide | ||
| + | } | ||
| + | |||
| + | *Construction des points fixes de la map donc les murs (probabilité 100) et les zones à risques (probabilité 50): | ||
| + | |||
| + | void Set_Wall(nav_msgs::OccupancyGrid &Map) | ||
| + | { | ||
| + | for (int i=0;i<80;i++) | ||
| + | { | ||
| + | for (int j=0;j<140;j++) | ||
| + | { | ||
| + | if ((i<13)||(i>67))) Map.data[j+i*140]=100; | ||
| + | if ((j<13)||(j>127)) Map.data[j+i*140]=100; | ||
| + | } | ||
| + | } | ||
| + | ... | ||
| + | } | ||
| + | |||
| + | Nous ne mettons pas tout le code de cette fonction étant donné qu'il est long et répétitif puisque c'est le remplissage des données connues, donc en "dur". | ||
| + | |||
| + | *Calcul des positions machines: | ||
| + | |||
| + | Lorsqu'on reçoit une position machine, c'est en fait son centre et son orientation par rapport à x que l'on reçoit. Etant donné que les machines doivent être des rectangles de 110cm sur 75cm (réellement 70 x 35 mais on compte la moitié du robot en plus par sécurité), on décide d'abord de déterminer un des coins du rectangle et plus précisément le coin en bas à droite de ce dernier: | ||
| + | |||
| + | void Get_One_Point_Of_The_Rectangle(float x, float &xA, float y, float &yA, float theta, float largeur, float longueur) | ||
| + | { | ||
| + | float x1,y1; | ||
| + | x1 = x - cos(theta)*longueur; | ||
| + | y1 = y - sin(theta)*longueur; | ||
| + | xA = x1 + sin(M_PI_2-theta)*largeur; | ||
| + | yA = y1 - cos(M_PI_2-theta)*largeur; | ||
| + | |||
} | } | ||
| − | == | + | *Remplissage des positions sur la map : |
| + | |||
| + | On met alors tous les points de ce rectangle à une probabilité 100 dans le vecteur Map. Pour les calculs on différencie le cas ou l'angle de la machine est entre 0 et pi/2 et le cas où il est entre pi/2 et pi. L'algorithme est le suivant : | ||
| + | |||
| + | A partir du coin, on incrémente x et y de sorte à longer le grand coté et de remplir chaque case (incrémentation de 5 cm). | ||
| + | Une fois arrivé au bout, on incrémente x et y de 5cm sur la largeur à partir du coin et on recommence l'opération précédente. | ||
| + | Ceci jusqu'à remplir le complètement le rectangle. | ||
| + | |||
| + | Afin d'établir les probabilités correspondantes aux cases de ce rectangle, nous utilisons la fonctions floor() pour "convertir" nos flottants en entier et accéder à la case correspondante. On notera aussi que la case 1470 correspond à l'origine de notre map. | ||
| + | |||
| + | void Set_Machines_In_Map(float rank, float theta, float xA, float yA, nav_msgs::OccupancyGrid &Map) | ||
| + | { | ||
| + | float x=xA; | ||
| + | float y=yA; | ||
| + | if (theta<=M_PI_2) | ||
| + | { | ||
| + | for (int j=0;j<10;j++) | ||
| + | { | ||
| + | for (int i=0;i<18;i++) | ||
| + | { | ||
| + | Map.data[1470+floor(x/rank)+floor(y/rank)*140]=100; | ||
| + | x = x + cos(theta)*50; | ||
| + | y = y + sin(theta)*50; | ||
| + | } | ||
| + | x = xA - j*cos(M_PI_2-theta)*50; | ||
| + | y = yA + j*sin(M_PI_2-theta)*50; | ||
| + | } | ||
| + | } | ||
| + | if (theta>M_PI_2) | ||
| + | { | ||
| + | for (int j=0;j<10;j++) | ||
| + | { | ||
| + | for (int i=0;i<18;i++) | ||
| + | { | ||
| + | Map.data[1470+floor(x/rank)+floor(y/rank)*140]=100; | ||
| + | x = x - sin(theta-M_PI_2)*50; | ||
| + | y = y + cos(theta-M_PI_2)*50; | ||
| + | } | ||
| + | x = xA - j*cos(theta-M_PI_2)*50; | ||
| + | y = yA - j*sin(theta-M_PI_2)*50; | ||
| + | } | ||
| + | } | ||
| + | } | ||
| + | |||
| + | Ci dessous on a les mains, avec les différentes fonctions appelées et la syntaxe particulière à ROS. | ||
| + | |||
| + | *Noeud général pour le traitement et le remplissage de la map : | ||
| + | |||
| + | /*========== Main ==========*/ | ||
| + | int main(int argc, char **argv) | ||
| + | { | ||
| + | ros::init(argc, argv, "server"); | ||
| + | ros::NodeHandle n; | ||
| + | ros::Subscriber sub_poses_machine = n.subscribe("/machines", 1000, Poses_Machine_Callback); // Récupération des machines | ||
| + | ros::Publisher Map_Pub = n.advertise<nav_msgs::OccupancyGrid>("/map", 1000); // Préparation de la publication de la map | ||
| + | ROS_INFO("Ready to Generate the Map"); | ||
| + | float xA,yA; | ||
| + | ros::Rate loop_rate(1); | ||
| + | while(ros::ok()) | ||
| + | { | ||
| + | nav_msgs::OccupancyGrid Map; | ||
| + | Create_Empty_Map(Map); | ||
| + | Set_Wall(Map); | ||
| + | for (int z=0;z<tab.size();z++) | ||
| + | { | ||
| + | Get_One_Point_Of_The_Rectangle(tab[z].x, xA, tab[z].y, yA, tab[z].theta, 275, 450); | ||
| + | Set_Machines_In_Map(100, tab[z].theta, xA, yA, Map); | ||
| + | } | ||
| + | Map_Pub.publish(Map); // publication de la map | ||
| + | ros::spinOnce(); | ||
| + | loop_rate.sleep(); | ||
| + | } | ||
| + | return 0; | ||
| + | } | ||
| + | |||
| + | |||
| + | *Noeud test qui publie 2 positions de machines : | ||
| + | |||
| + | /*========== Main ==========*/ | ||
| + | int main(int argc, char **argv) | ||
| + | { | ||
| + | ros::init(argc, argv, "test"); | ||
| + | ros::NodeHandle n; | ||
| + | ros::Publisher Pose_Machines_Pub = n.advertise<deplacement_msg::Landmarks>("/machines", 1000); | ||
| + | ROS_INFO("Ready to send poses machines"); | ||
| + | int xA,yA; | ||
| + | ros::Rate loop_rate(1); | ||
| + | while(ros::ok()) | ||
| + | { | ||
| + | deplacement_msg::Landmarks machines_msgs; | ||
| + | geometry_msgs::Pose2D tab; | ||
| + | tab.x=-2; | ||
| + | tab.y=2; | ||
| + | tab.theta=0; | ||
| + | machines_msgs.landmarks.push_back(tab); | ||
| + | tab.x=5; | ||
| + | tab.y=4; | ||
| + | tab.theta=2.5; | ||
| + | machines_msgs.landmarks.push_back(tab); | ||
| + | Pose_Machines_Pub.publish(machines_msgs); | ||
| + | ros::spinOnce(); | ||
| + | loop_rate.sleep(); | ||
| + | } | ||
| + | return 0; | ||
| + | } | ||
| + | |||
| + | On visualise le résultat grâce au logiciel RVIZ qui peut lire les topics publiés et donc le topic /map : | ||
| + | |||
| + | [[Fichier:Mapcompet.PNG|thumb|center]] | ||
| + | |||
| + | ===Semaine 9=== | ||
| + | |||
| + | ====Localisation - Extended Kalman Filter==== | ||
| + | |||
| + | l'objectif de cette semaine sera de coder toutes les fonctions nécessaires à l'implémentation finale du [http://fr.wikipedia.org/wiki/Filtre_de_Kalman#Filtre_de_Kalman_.C3.A9tendu filtre de Kalman étendu] : | ||
| + | |||
| + | *initialisations des différents éléments | ||
| + | *étape de prédiction | ||
| + | *étape de mise à jour | ||
| + | *publication des positions machines et du robot dans le repère global via un topic ROS | ||
| + | |||
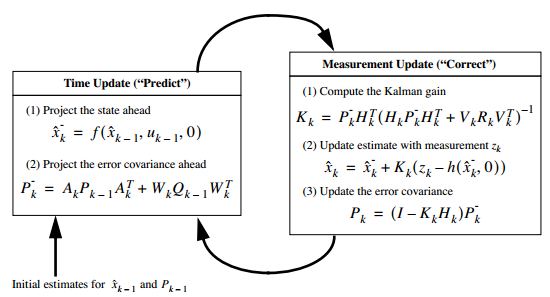
| + | Le schéma ci-dessous nous montre les deux étapes du filtre de Kalman : | ||
| + | |||
| + | [[Fichier:Kalman.png | center]] | ||
| + | |||
| + | le code pour la partie ''prédiction'' : | ||
| + | |||
| + | //on ressort la position du robot pour l'état n+1 | ||
| + | //les paramètres sont le vecteurs où on a la position du robot à l'état n, la matrice P, les commandes en vitesses et le temps à l'état n | ||
| + | Vector3d prediction(VectorXd xMean, MatrixXd &P, geometry_msgs::Pose2D cmdVel, ros::Time &temps){ | ||
| + | ros::Duration duree = ros::Time::now() - temps; | ||
| + | double periode = duree.toSec();<br> | ||
| + | Vector3d cmdVelVect = Pose2DToVector(cmdVel); | ||
| + | //le xMean.topLeftCorner(3,1) correspond à la position du robot | ||
| + | Vector3d xPredicted = xMean.topLeftCorner(3,1) + periode*cmdVelVect;<br> | ||
| + | MatrixXd Fx; | ||
| + | Fx = MatrixXd::Identity(P.rows(), P.cols()); | ||
| + | Fx(0,0) = xPredicted(0); | ||
| + | Fx(1,1) = xPredicted(1); | ||
| + | Fx(2,2) = xPredicted(2);<br> | ||
| + | //mise à jour de P | ||
| + | P = Fx*P*(Fx.transpose());<br> | ||
| + | //mise à jour du temps | ||
| + | temps = ros::Time::now();<br> | ||
| + | return xPredicted; | ||
| + | } | ||
| + | |||
| + | le code pour la partie ''correction'' : | ||
| + | |||
| + | void correction(VectorXd &xMean, MatrixXd &P, Vector3d xPredicted, geometry_msgs::Pose2D m){ | ||
| + | int taille = P.rows(); | ||
| + | //on vérifie si la machine est présente ou pas dans le vecteur d'état | ||
| + | int i = checkStateVector(xMean, m);<br> | ||
| + | if (i != 0){ | ||
| + | //calcul de H | ||
| + | MatrixXd H(3, taille); | ||
| + | H = buildH(taille, i);<br> | ||
| + | //calcul de Pm | ||
| + | MatrixXd Pm(taille, taille); | ||
| + | Pm = buildPm(P, i);<br> | ||
| + | //calcul de Z | ||
| + | MatrixXd Z(taille, taille); | ||
| + | Z = H*Pm*(H.transpose()); <br> | ||
| + | //calcul du gain de Kalman | ||
| + | MatrixXd K(taille, taille); | ||
| + | K = P*(H.transpose())*(Z.inverse());<br> | ||
| + | //mise à jour du vecteur xMean | ||
| + | xMean = xMean + K*(xMean.block(xMean.rows()-3,0,3,1) - xPredicted);<br> | ||
| + | //mise à jour de la matrice P | ||
| + | P = P - K*Z*(K.transpose()); | ||
| + | } | ||
| + | else { | ||
| + | addMachine(m, xMean, P); | ||
| + | } | ||
| + | } | ||
| + | |||
| + | Pour notre cas, on doit ajouter des nouvelles machines, alors que pour un EKF classique on observe juste des machines déjà répertoriées. Il faut donc une fonction qui permet d'ajouter une machine dans le vecteur d'état. La voilà : | ||
| + | |||
| + | void addMachine(geometry_msgs::Pose2D machine, VectorXd &xMean, MatrixXd &P){ | ||
| + | //on redimensionne xMean et P pour accueillir la nouvelle machines | ||
| + | xMean.conservativeResize(xMean.rows() + 3); | ||
| + | P.conservativeResize(P.rows()+3,P.cols()+3);<br> | ||
| + | //on remplit avec les coordonnées de la nouvelle machine | ||
| + | xMean(xMean.rows()-3) = machine.x; | ||
| + | xMean(xMean.rows()-2) = machine.y; | ||
| + | xMean(xMean.rows()-1) = machine.theta;<br> | ||
| + | //calcul de tous les PLi | ||
| + | //initialisation des PLi à 0 | ||
| + | P.block(P.rows() - 3, 0, 3, P.cols()).setZero(); | ||
| + | P.block(0, P.cols() - 3, P.rows(), 3).setZero();<br> | ||
| + | for (int j = 0; j < xMean.rows(); j = j + 3){ | ||
| + | //position de la nouvelle machines par rapport au robot et à toutes les autres | ||
| + | double x = xMean(xMean.rows()-3) - xMean(j ); | ||
| + | double y = xMean(xMean.rows()-2) - xMean(j+1); | ||
| + | double theta = xMean(xMean.rows()-1) - xMean(j+2);<br> | ||
| + | P(P.rows()-3, j ) = x; | ||
| + | P(P.rows()-2, j+1) = y; | ||
| + | P(P.rows()-1, j+2) = theta;<br> | ||
| + | P(j , P.rows()-3) = x; | ||
| + | P(j+1, P.rows()-2) = y; | ||
| + | P(j+2, P.rows()-1) = theta;<br> | ||
| + | P(j , j ) = xMean(j ) - xMean(0); | ||
| + | P(j+1, j+1) = xMean(j+1) - xMean(1); | ||
| + | P(j+2, j+2) = xMean(j+2) - xMean(2);<br> | ||
| + | } | ||
| + | } | ||
| + | |||
| + | ===Semaine 10=== | ||
| + | |||
| + | ====Localisation - Extended Kalman Filter==== | ||
| + | |||
| + | La partie '''prédiction''' du filtre marche parfaitement, quelques corrections ont dues être faites au niveau de la commande vitesse. En effet, Nous avions oublié de la transposer dans le repère global. Pour la partie '''correction''', nous rencontrons un problème de divergence du filtre, qui est probablement due à une mauvaise initialisation. En effet, nous utilisons des enregistrements faits sur notre piste (1/4 de la vraie) avec des initialisations correspondant à la piste originale. Le filtre ne peut donc pas converger car la position de départ est fausse. | ||
| + | |||
| + | ===Semaine 11=== | ||
| + | |||
| + | ====Localisation - Extended Kalman Filter==== | ||
| + | |||
| + | Des corrections sont en cours de validation. Nous essayons de définir une initialisation avec les paramètres de notre piste, ce qui n'est pas évident. Les programmes permettant d'extraire les positions machines du filtres ont été réalisé, ainsi qu'un launch pour pouvoir lancer tous les noeuds de la localisation. | ||
| + | |||
| + | ===Semaine 12=== | ||
| + | |||
| + | ====Compétition Open German - mise en place==== | ||
| + | |||
| + | Pendant les deux jours de mise en place, nous avons continué à travailler sur la localisation, qui est une partie critique et nécessaire à notre participation. Le filtre en lui même est fonctionnel et permet de corriger la position du robot, ainsi que celle des machines. Cependant, et ce n'est pas un petit "cependant"... Le fait que l'on ajoute des machines en cours de jeu perturbe fortement notre algorithme. | ||
| + | |||
| + | En effet, le filtre de Kalman est optimal si la position des repères est connu, or, un ajout de machine crée un recalage forcé, et si l'on voit plusieurs machines... C'est la '''catastrophe'''. L'ajout de machines est une partie sensible qui nécessite des tests sur la position mesurée, avec un changement de repère à partir de la position du robot, si celle ci dérive, tout dérive. Chaque machine initialisée à la mauvaise position, ou chaque élément détecté comme machine mais n'en étant pas une (faux positif) perturbe le recalage. | ||
| + | |||
| + | De nombreux tests ayant été fait sur la piste officiel avec différentes configurations nous ont permis de vérifier que l'odométrie mesurée ne dérivait que très peu. Il a donc été décidé de n'utiliser que l'odométrie et le scan laser pour la partie '''exploration'''. En effet, chaque machine mesurée est envoyée à un noeud ROS qui va créer une carte et la compléter au fur et à mesure de la partie. Le robot est donc repéré rien qu'avec son odométrie. Le fait que la phase d'exploration (découverte du terrain) ne dure que '''4 minutes''' nous a convaincu pour n'utiliser que cette mesure. | ||
| + | |||
| + | De plus, la carte créée sera utilisée pour la phase suivante, la phase de '''production'''. Cette phase consiste, au niveau de la localisation, à se repérer sur la piste et atteindre la machine demandée par l'exécuteur de tâches. Pour cette phase qui dure '''15 minutes''', l'utilisation du filtre est nécessaire. Donc, avec les coordonnées des machines mesurées pendant la première phase, on peut créer le vecteur d'état et la matrice faisant le lien entre les machines. De là, la taille de ces deux éléments ne variant plus, on peut corriger uniquement la position du robot et le filtre sera efficace. | ||
| + | |||
| + | ====Compétition Open German - 1er jour==== | ||
| + | |||
| + | Durant ce premier jour, nous avons commencé à ''merger'' nos branches respectives pour pouvoir faire tourner tous nos programmes. Cette phase est laborieuse et nous a pris du temps. De toute façon, toutes les équipes ne sont pas prêtes, les organisateurs non plus. La '''Referee Box''' n'est pas fonctionnel pour la phase de production, ce qui veut dire que nous nous concentrons actuellement sur l'exploration. Les matchs joués aujourd'hui ne nous rapporte donc pas de points. Les tests nous ont permis de valider individuellement chacun des algos, il ne reste "plus qu'à" rejoindre le tout. | ||
| + | |||
| + | ====Compétition Open German - 2eme jour==== | ||
| + | |||
| + | Niveau '''localisation''', la navigation à l'odométrie et la détection de machine sont fonctionnelles. Cependant, le moyennage fait sur les positions machines (on moyenne toutes les positions trouvées appartenant à une même machine pour n'avoir qu'un seul point) fait que le point correspondant peut être perturbé par des mesures aberrantes. C'est le cas lorsque le robot se déplace à vitesse élevée. | ||
| + | |||
| + | La détection de machine a été améliorée afin de ne rajouter QUE les machines, et pas les murs de la même taille. Nous allons donc retester le '''filtre de Kalman Etendu''' avec cette amélioration. Cependant, ce ne sera fait qu'après la compétition, puisque d'autres problèmes ont nécessité la présence de l'équipe sur certaines parties sensibles du déplacement. | ||
| + | |||
| + | Sur la piste nous avons fait des mesures, qui nous donnent la carte suivante : | ||
| + | |||
| + | [[Fichier:PisteSamediSoir.PNG | center]] | ||
| + | |||
| + | La visualisation du trajet pour découvrir ces machines est le suivant : | ||
| + | |||
| + | [[Fichier:DetectionSamediSoir.PNG | center | thumb]] | ||
| + | |||
| + | Et les positions machines, ainsi que leur orientation sont les suivantes : | ||
| + | |||
| + | [[Fichier:MachinesBagtestSamediSoir.PNG | center | thumb]] | ||
| + | |||
| + | ====Compétition Open German - 3eme et dernier jour==== | ||
| + | |||
| + | L'architecture choisie pour la localisation est la suivante : | ||
| + | *Navigation à l'odométrie | ||
| + | *Détection de machines et moyennage | ||
| + | *Quand on a vu toutes nos machines, on utilise la symétrie pour compléter les machines restantes | ||
| + | *Navigation et Localisation avec l'EKF (correction des positions machines et du robot) | ||
| + | |||
| + | ====Localisation - Extended Kalman Filter==== | ||
| + | |||
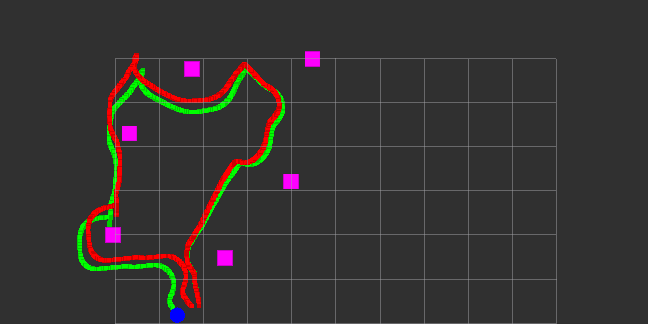
| + | Après de longs tests et des corrections importantes au niveau de l'ajout des machines dans le filtre, ce qui était la partie critique... Le meilleur résultat que l'on ait pu avoir avec l'EKF est celui ci dessous. Les machines étant en <span style="color:#9966CC">violet</span>, la trajectoire calculée par l'EKF en <span style="color:#00FF00">vert</span> et la trajectoire mesurée par les codeurs en <span style="color:red">rouge</span>. | ||
| + | |||
| + | [[Fichier:BestResultWithEKF.PNG | center]] | ||
| + | |||
| + | Nous rappelons que tous nos codes sont disponibles sur notre [https://github.com/PyroTeam/robocup-pkg/tree/navigation-devel/navigation/localisation GIT]. | ||
| + | |||
| + | ====Video==== | ||
| + | |||
| + | |||
| + | Enfin, afin d'illustrer nos résultats de manière ludique et attrayante, voici une vidéo qui vous donnera goût à la RoboCup ! | ||
| + | |||
| + | https://www.youtube.com/watch?v=PB6g2krvCFI | ||
| + | |||
| + | [[Fichier:RapportProjetDanelKrikorian.pdf]] | ||
Version actuelle datée du 15 juin 2015 à 13:01
Sommaire
Cahier des charges
Présentation générale du projet
Avec plusieurs IMAs, nous avons créer une équipe pour participer à la Logistic League de la RoboCup. Lors de la compétition de l'Open German, version européenne de la RoboCup, il faudra mettre en place un système autonome de production à l'aide de Robotinos (robots mobiles de Festo ayant un système d'exploitation Linux) afin de réaliser des produits en fonction des demandes de l'arbitre du jeu : la Referee Box. Nous traiterons dans ce projet de l'aspect navigation des robots, composé d'une partie localisation et d'une partie déplacement.
Contexte
La compétition de l'Open German se déroule en quatre phases spécifiques : phase de début-de-jeu, phase d'exploration, phase de production, phase de fin-de-jeu. La navigation sera utilisée dans la phase d'exploration afin de réaliser une carte de la zone de jeu permettant de définir des zones de passage entre les machines. Dans la phase de production, la navigation permettra de se déplacer à partir de la carte créée au préalable (avec les obstacles fixes) et des robots (obstacles mobiles) se déplaçant en même temps.
Objectif du projet
Fournir aux Robotinos un système capable de se localiser et de parcourir des trajectoires calculées à partir de coordonnées envoyées par le Manager.
Description du projet
- Localiser correctement le robot (à 5 cm près)
- Localiser les éléments fixes :
- Murs
- Machines
- Générer une trajectoire selon :
- les demandes du "Manager"
- la détection d'obstacles dynamiques (robots)
- Assurer le suivi de la trajectoire
Choix techniques : matériel et logiciel
- Utilisation de 3 Robotinos équipés chacun de :
- 1 détecteur laser pouvant réaliser des mesures à 240°
- 1 gyroscope
- 9 capteurs SHARP (télémètres infrarouges)
- 3 codeurs incrémentaux présents en sortie de chaque moteur du Robotino
- Utilisation de ROS Hydro
- Utilisation de différents langages : C++ ou Python
- Utilisation de Linux Ubuntu 12.04
Etapes du projet
- Conception du schéma global des différentes parties :
- Localisation avec le SLAM
- Création de la carte avec le SLAM
- Génération de trajectoire avec A-Star
- Execution de trajectoire avec le noeud ROS pour Robotino robotino_local_move
- Codage des différents noeuds ROS
- Tests de précision et de robustesse sur robot
- Validation du modèle
- Améliorations possibles :
- Fusionner les maps des 3 robots
- D-Star Lite au lieu de A-Star
- Filtrage des données laser
Avancement du Projet
Semaine 1
- Participation aux Finales Nationales des Olympiades des Métiers en robotique mobile (4ème)
Semaine 2
Etablissement du cahier des charges
- Prise de connaissance des contraintes d'environnement
- Dialogue avec l'équipe responsable de la partie Manager
- Familiarisation avec l'environnement logiciel ROS
- Recherches de solutions pour la localisation (SLAM)
- Recherche de solution pour la génération de trajectoire (algorithme A-star)
Recherche d'un algorithme de recherche de chemin
Nous avons fait nos recherches en nous orientant sur le déplacement du Robotino afin de trouver un algorithme de recherche de chemin, capable de trouver le chemin le plus court, puisqu'un des buts de la compétition étant la rapidité.
Plusieurs algorithmes sont donc ressortis :
- L'algorithme Dijkstra (On part du point de départ et on cherche le chemin le plus court vers le point d'arrivée en cherchant dans TOUTES les directions)
- L'algorithme A-Star (Basé sur Dijkstra, cet algo s'oriente directement vers le point d'arrivée en minimisant la distance avec celui-ci)
- L'algorithme D-Star Lite (Amélioration du A-Star avec bufferisation des précédents calculs pour éviter les calculs inutiles en cas d'arrivée d'un obstacle mobile sur la trajectoire)
Nous avons visualisé les différents algorithmes sur PathFinding
Fonctionnement de l'algorithme A-Star :
- Tout d'abord, on calcule la distance qui sépare le robot du point d'arrivée, et on définit les points interdits par les obstacles. (la zone bleue correspond
à l'obstacle et la zone verte est une zone ou le robot touche l'obstacle. Ces deux zones constituent la zone interdite).
- Ensuite le Robot trouve un premier noeud sur la grille qu'on lui a attribué. Si le noeud n'est pas dans une zone interdite, il sauvegarde ce noeud.
- Il répète l'opération jusqu'à trouver le chemin qui le mènera à l'arrivée
- Attention : c'est seulement lorsqu'il aura trouvé le chemin complet que le robot va se déplacer !
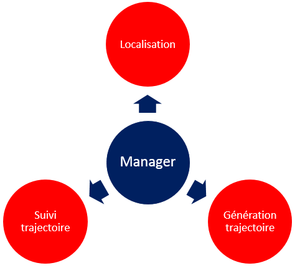
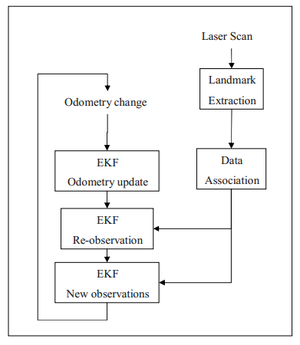
Recherche d'une solution pour la localisation
Pour la localisation nous allons utilisé un Algorithme de Localisation et Cartographie Simultanée (SLAM en anglais):
Explicitation des différentes parties :
- Odometry change : changement de position
- Odometry update : mise à jour de l'odométrie
- Re-observation : vérification des changements à partir de toutes les données disponibles
- New observations : mise à jours de la matrice d'état
- Laser scan : scan laser brut
- Landmark Extraction : extraction des objets caractéristiques
- Data Association : association entre objets scannés et objets en mémoire
Ce schéma sera explicité à la séance prochaine.
Semaine 3
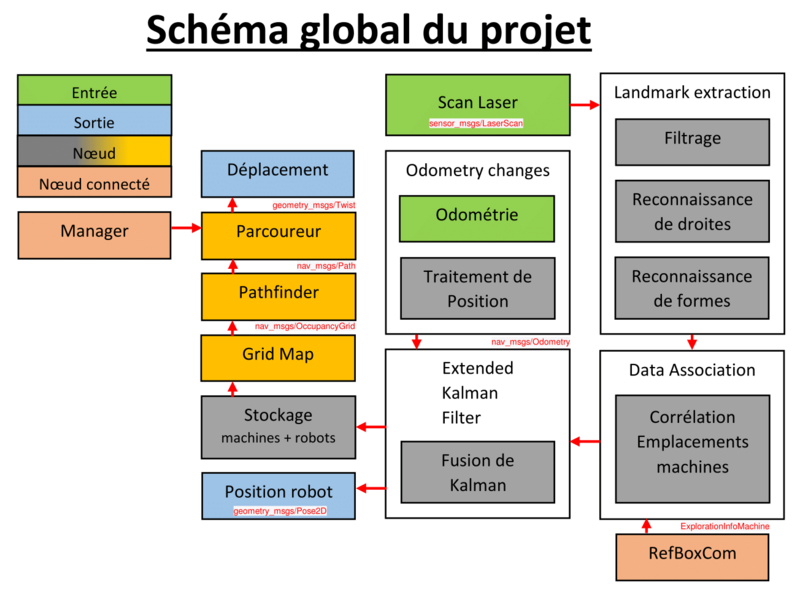
Découpage du travail à effectuer
Nous avons découper le travail de génération de map et de la correction de position de la manière suivante :
( Nous recommandons au lecteur de se référer à la partie vocabulaire pour comprendre les termes techniques )
Chaque case du diagramme précédent correspond à un noeud ROS.
Décrivons précisément le rôle de chaque noeud :
- Laser récupère les données brutes du laser.
- Filtrage permet, comme son nom l'indique, d'enlever les éventuels bruits qui affectent les données du laser.
- Reconnaissance des droites traite les données laser filtrées pour détecter les droites présentes (Transformée de Hough ou Ransac)
- Reconnaissance des formes extrapole les objets (machines) à partir des droites.
- Corrélation emplacements machines lie la position des machines détectées au laser et les positions envoyées par RefBoxCom pour éviter les incohérences.
- Odométrie récupère la position du robot par rapport au point de départ. Il renvoie une position corrigée grâce au gyroscope(Pose) et une position non corrigée par le gyroscope (Twist)
- Traitement de position corrige l'erreur sur le Twist avec les données du gyroscope (par dérivation).
- Fusion de Kalman est un algorithme qui va coupler les données de position et les données du laser afin de fournir un modèle et une position précise. C'est le noeud central du SLAM.
- Stockage machines + robot transforme les positions des machines et du robot en grille. Il sera couplé aux détections d'obstacles.
- Grid Map renvoit une map utilisée ensuite pour les déplacements et les calculs de trajectoires (A_Star)
- RefBoxCom stocke et renvoie la position des machines.
- Position robot renvoie la position exacte du robot sur la grille.
- Manager Noeud qui envoie la position à atteindre.
- Pathfinder recherche le chemin demandé par le Manager sur une grille
- Parcoureur exécute le chemin trouvé en fournissant les vitesses au noeud Déplacement.
- Déplacement (noeud robotino_local_move_server), qui donne les commandes aux moteurs à partir de la vitesse linéaire et angulaire envoyée par le Parcoureur.
Recherche de documentation sur ROS et l'API du Robotino
Nous avons cherchés toutes les documentations techniques nécessaires pour la programmation de chaque noeud : Wiki_ROS et API_Robotino, nous permettant de mettre à jour le schéma global, notamment au niveau des types.
Etude de l'algorithme A-star précédent
Nous nous sommes ensuite concentrés sur le noeud GridMap qui contient Map.cpp :
Dans le code de l'an dernier, ce noeud générait une grille en dur. Cependant, cette solution n'est pas possible cette année car nous ne connaissons pas toutes les informations sur la piste (on connaît à peu près la position mais pas l'orientation). Il va donc falloir générer une grille en fonction du noeud précédent qui nous renverra un type OccupancyGrid.
Etant donné que ce noeud tournera en permanence, si des informations changent pendant que le robot est sur la piste (détection des nouvelles machines par exemple), le noeud Map.cpp modifiera la grille en temps réel.
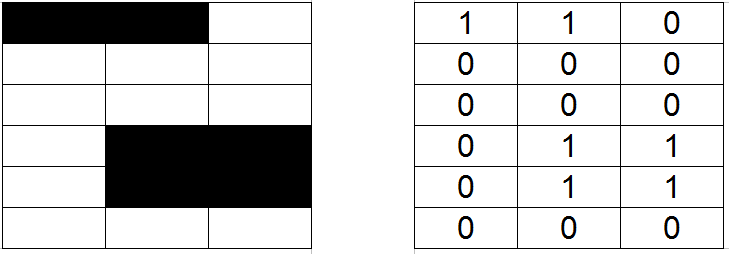
La grille est décomposée en case pour le A-Star :
Si c'est une case interdite (obstacle) ont associe a la case la valeur 1, si elle est autorisée, on associe la valeur 0. On illustre le principe précédent par un exemple :
Cependant, le noeud "Grid Map" va nous délivrer un vecteur et non une matrice par le biais de OccupancyGrid.Data.Dans notre exemple précédent, on récupère le vecteur suivant :
On choisit donc de transformer ce vecteur en matrice, car l'algorithme A-Star fonctionne sur un graphe, pas un vecteur. On connait la largeur (en case) de la grille grâce au type OccupancyGrid.info.width.
Le pseudo-code pour générer la matrice à partir de ce vecteur sera le suivant :
fonction create_grid (OccupancyGrid.Data vecteur[size]) : matrice[height].[width]
{
matrice[height].[width] ;
int t <- size;
Pour (i de 0 à height)
faire:
{
Pour (j de 0 à width)
faire :
{
matrice[i].[j] <- vecteur[t] ;
t++;
}
}
return matrice;
}
Semaine 4
Localisation - Landmarks Extraction
Nous nous concentrons essentiellement sur la première partie, qui est la partie : "Landmarks Extraction" (extraction des points de repères). On travaille ici dans le repère du laser, qui est différent de celui du robot, et du global. La transposition dans le repère global se fera dans la partie "Data Association". On doit ainsi, dans l'ordre :
☑ récupérer des données lasers via le topic /scan
☑ convertir les coordonnées polaires en coordonnées cartésiennes en filtrant les données aberrantes (> range_max et < range_min)
☑ implémenter l'algorithme RANSAC (Random SAmple Consensus) de détection de droites :
☑ détecter la "meilleure" droite à partir des points en sélectionnant aléatoirement des combinaisons de points
☑ stocker le meilleur modèle (angle + tableau de points)
☑ recommencer tant qu'il reste assez de points à traiter (5)
☑ extraire les segments à partir des modèles trouvés et des points
☑ extraire les points extrèmes
☑ calculer la taille du segment
☑ chercher des angles droits, des segments de 35 ou 70 cm (largeur et longueur d'une machine)
☑ extrapoler les positions des machines dans le repère du laser
☑ définir le barycentre de la machine ainsi que son angle
☐ stocker ces positions
Pathfinder
Nous avons aussi pris du temps avec Valentin VERGEZ, qui a développé, l'an dernier, les codes pour le déplacement du Robotino et le calcul de trajectoire
Nous avons éclairci quelques points sur cette partie du projet :
- Les commentaires sur l'utilité de chaque fonction ont été rajoutés.
- Le "code mort" a été nettoyé ainsi que les parties inutiles.
- Nous devons trouver un moyen de tester cette partie du code seule. (A priori graphiquement).
Etant donné l'arrivée d'un nouvel ordinateur au sein de l'équipe, nous en avons profités pour installer les logiciels qui nous permettrons de faire tourner les noeuds codés sur les Robotino :
- Installation d'Ubuntu 12.04 ( c'est cette version qui permet de faire tourner ROS Hydro)
- Installation de ROS Hydro (ensemble d'outils informatiques open source permettant de développer des logiciels pour la robotique.)
- Installation des paquets nécessaires (catkin, Desktop Install, ROS-Base, Individual Package)
- Installation de GIT (outil de bas niveau permettant de gérer l'évolution du contenu d'une arborescence)
- Vérification que toutes les fonctionnalités de ROS Hydro étaient présentes ( Tutoriel)
La récupération du code complet de l'année dernière et une solution a été trouvée afin de tester le code de génération de trajectoire A-star:
- Pour visualiser une Map ainsi qu'un Path (chemin), on peut utiliser l'outils RVIZ.
- Dans RVIZ, on peut ajouter un Path (topic /path), ainsi qu'ajouter une Map (/grid): Ceci correspond exactement à ce que nous souhaitons visualiser pour la partie calcul de trajectoire.
- Pour publier une Map fictive, on executera le script fakeGrid.sh
- Pour générer un chemin, on lancera le pathfinder (rosruns rbqt_pathfinder server : notre code) et on effectuera une requête avec le script pathReq.sh.
Si tout se passe correctement, le chemin devrait s'afficher en vert sur la map.
Nous avons aussi du communiquer notre avancement aux autres parties de l'équipe. Le schéma général ainsi qu'un outil permettant d'expliquer les différents algorithmes de recherche de trajectoire optimale nous ont aidé à leur communiquer nos objectifs et les processus choisis.
L'algorithme A-Star que nous allons utiliser donne le résultat final suivant (utilisation du site PathFinding ):
- le chemin optimal calculé par A-Star
- le point de départ
- le point d'arrivée
- les points interdits (obstacle)
- les points que l'algorithme a déjà calculé
- les points que l'algorithme aurait calculé à la prochaine itération
Localisation - Landmarks extraction - filtrage
Dans cette partie, nous avons commencé à définir une classe laserScan qui contient la fonction polarToCart, elle convertit les données laser (tableau de ranges) en liste de points (x,y) :
void laserScan::PolarToCart (){
Point p;
for (int i=0; i<m_ranges.size(); i++){
if((m_ranges[i]>getRangeMin()) && (m_ranges[i]<getRangeMax())){
p.setX(m_ranges[i]*cos(getAngleMin() + i*getAngleInc()));
p.setY(m_ranges[i]*sin(getAngleMin() + i*getAngleInc()));
m_points.push_back(p);
}
}
}
Localisation - Landmarks extraction - reconnaissance de droite
Dans cette partie, nous avons déterminé quel algorithme nous allons utiliser : RANSAC. L'algorithme de RANSAC trouve la meilleure droite dans un nuage de points. On itère plusieurs fois cet algorithme afin de trouver l'ensemble de toutes les droites du scan laser. On a donc en sortie une liste des droites composants le nuage de points initial.
Entrée : listOfPoints -> liste de points initiale
Sortie : meilleur_modèle -> les paramètres de la droite qui correspondent le mieux aux points
-> tableau de points à partir desquels la droite a été estimée
-> erreur du modèle de droite par rapport aux points
tant que la liste contient assez de points itérateur := 0 meilleur_modèle := aucun tant que itérateur < k (fixé par une loi de probabilité) on choisit deux points au hasard dans la liste on fabrique un modèle_possible à partir de ces deux points Pour chaque point de la liste qui ne sont pas dans le modele_possible si le point s'ajuste au modele_possible avec une erreur inférieure à t Ajouter ce point au modele si le nombre de points dans le modele est suffisant pour valider l'existence du modele erreur := coefficient de corrélation de la régression linéaire de ensemble_points si erreur < erreur du meilleur_modele meilleur_modèle := modèle_possible
stocker meilleur_modèle dans liste de modèles retirer meilleur_ensemble_points de la liste des points initiale recommencer avec la liste modifiée
Semaine 5
Localisation - Landmarks Extraction - reconnaissance de droite
Nous avons adapté l'algorithme précédent afin de mieux correspondre aux structures que nous avons créées :
- Modele
- Liste de points
- Liste d'indices
- Corrélation
- Droite
- Point
- Angle
- Segment
- Point "min"
- Point "max"
- Angle
- Taille
Nous avons aussi codé toutes les fonctions nécessaires dans l'algorithme de Ransac, dont celle permettant la correction de l'approximation de droite par régression linéaire des points correspondants à un modèle trouvé (linReg()) qui nous a donné matière à réflexion. Aussi, notre première idée qui était de travailler avec des std::vector a du changer puisque l'aspect récursif de l'algorithme que nous allons utiliser nécessite de multiples suppressions sur les données à entrer dans l'algorithme de Ransac. On travaille donc maintenant avec des std::list.
Tous nos codes sont disponibles sur la branche feature/navigation/SLAM du GIT de l'équipe PyroTeam.
Semaine de vacances de février
Localisation - Landmarks Extraction - reconnaissance de droite
Nous devons réaliser un noeud permettant de valider notre algorithme, c'est-à-dire implémenter sous ROS notre code C++ afin de tester, soit directement sur le robot, soit avec des bagfiles. Cette étape est très importante pour pouvoir passer à la suite : extrapoler les droites trouvées en segments puis en objets.
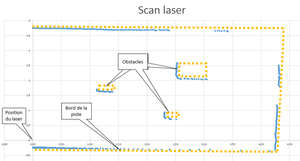
Notre programme consistant à reconnaître les droites à partir du scan laser est fonctionnel et a été testé à partir du scan laser suivant :
Processus de validation :
- Lancer le programme rosrun localisation test_polar_to_cart
résultat : on trouve 5 droites
m = -0.0229637 p = -0.24079 nb de points dans la droite : 246 coeff de correlation : 0.812376
m = -0.0315132 p = 3.7506 nb de points dans la droite : 102 coeff de correlation : 0.928089
m = 32.9243 p = -139.943 nb de points dans la droite : 77 coeff de correlation : 0.914475
m = 7.04634 p = -15.42 nb de points dans la droite : 32 coeff de correlation : 0.970724
m = 0.253029 p = 1.32235 nb de points dans la droite : 28 coeff de correlation : 0.979578
ce qui correspond à l'image suivante :
On voit que la recherche de droite marche bien, mais peut être améliorée en ajoutant des conditions de proximité des points correspondants à une seule droite, pour éviter le phénomène que l'on voit au milieu. Le résultat après avoir ajouté cette condition et en ayant affiné au maximum les paramètres, au dépend d'un temps de calcul beaucoup plus élevé (9,416 secondes au lieu de 0,536 s) :
Les impératifs de la compétition nous imposant une certaine rapidité pour se localiser et détecter les machines, nous retiendrons la solution la plus rapide et nous séparerons les droites en segment après leur détection.
Pour valider l'algorithme de régression linéaire nous avons :
- Récupéré tous les points correspondants à chaque droite
- Rentré ces points sur Excel
- Fait une courbe de tendance
- Affiché l'équation de droite et le coefficient de corrélation
- Comparé avec ce qu'a trouvé notre programme
- Conclu que notre programme était bon
Semaine 6
Localisation - Landmarks Extraction - reconnaissance de machines
Les objectifs de cette semaine :
- à partir de la liste de droites, extraire les segments
- extrapoler les positions machines à partir d'un segment complet (35 ou 70 cm)
- réaliser une interface graphique pour visualiser les segments trouvés en temps réel
- regarder ce qu'on doit rentrer dans l' Extended Kalman Filter au niveau du format des positions machines et de l'odométrie pour pouvoir réaliser le Data Association de façon cohérente avec la suite.
L'extraction de segment à partir des 5 droite précédemment trouvées nous donne 7 segments:
Segment 1
Min(-1.04033e-08, -0.238) Max(4.24699, -0.26092) taille : 4.24705 angle : -0.309205
Segment 2
Min(-1.64267e-07, 3.758) Max(3.4172, 3.63358) taille : 3.41946 angle : -2.08521
Segment 3
Min(4.24452, -0.234635) Max(4.33124, 2.18017) taille : 2.41636 angle : 87.9432
Segment 4
Min(2.30055, 0.871242) Max(2.32511, 0.736592) taille : 0.136872 angle : -79.6622
Segment 5
Min(2.50359, 2.18655) Max(2.53413, 2.56542) taille : 0.380104 angle : 85.3914
Segment 6
Min(2.73122, 2.05171) Max(3.049, 2.03728) taille : 0.318107 angle : -2.5999
Segment 7
Min(1.14156, 1.64221) Max(1.39648, 1.61891) taille : 0.255984 angle : -5.22068
Tout cela en 0,540s !
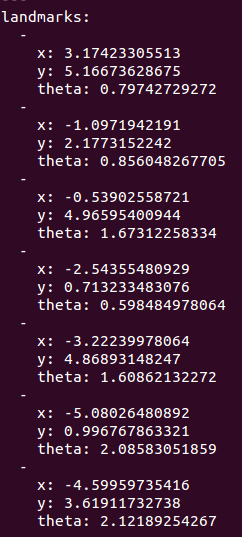
A partir de la liste de segments précédente, on extrait une liste de machine à partir des segments de 35 ou 70 cm, qui sont les tailles des machines. Comme le scan que nous utilisons pour le moment n'est pas un scan avec une vraie machine, mais disposant quand même de 2 segments d'à peu près 35 cm, nous utilisons ces deux segments comme petit côté de la machine. On trouve ainsi deux machines :
Machine 1 centre en (2.53292, 2.20155) orientation : 175.391°
Machine 2 centre en (3.06493, 2.05243) orientation : 87.4001°
Une amélioration de l'algorithme a été faite pour la détection de machine. En effet, dans le cas où on détectait un petit et un grand côté de machine, on trouvait deux machines avec des centres à peu près au même endroit. Maintenant, on fusionne ces données en créant un point milieu entre les deux données, et on prend l'orientation du grand côté.
On a commencé à faire des tests sur ROS directement avec un noeud factice qui publie un scan laser à une fréquence de 10Hz, ce qui est la fréquence réelle du laser Hokuyo. La détection se fait assez rapidement et de façon précise. Des tests sur le robot sont prévus en début de semaine 7 avec les vraies machines.
Semaine 7
Localisation - Data Association
L'objectif principal de cette semaine est de coder le noeud Data Association qui liera la position donnée par l'odométrie (mesure relative de la position par rapport à un point de départ à peu près connu) avec les machines trouvées dans le champ du laser.
Il faudra aussi corriger l'odométrie donné par le nœud robotino_odometry_node, qui donne l'odométrie (mesure de la position et de la vitesse du robot). Le problème est que nous utilisons un gyroscope externe, car le gyroscope de base est de très basse qualité. Or, si le nœud corrige parfaitement la position, il ne corrige pas du tout la vitesse angulaire ! Nous devons donc réaliser un nœud qui le fera pour nous.
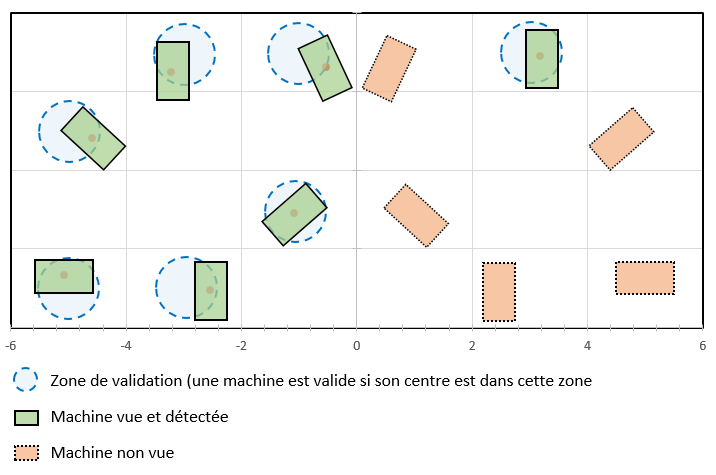
D'après la dernière version du sujet 2015, l'aire de jeu de 6 x 12 m est séparée en zones de 1,5 x 2 m de large, dans lesquelles se situent une seule machine. Chaque équipe a 6 machines dont la zone est connue, donnée par la Referee Box. Le but du nœud ROS de Data Association sera de transposer les positions machines dans le repère global de la piste, ainsi le Manager pour savoir devant quelle machine le robot est, et connaître sa position et son orientation.
La piste sera donc comme cela :
La correction d'odométrie a fait apparaître une erreur de mesure d'environ 1,7°/s sur la vitesse angulaire, à faible vitesse. Pour de la Localisation et Cartographie Simultanée, c'est assez important. Ça justifie donc la nécessité de faire cet ajustement.
Pour la suite, il a été décidé de fusionner les nœuds Data Association et Extended Kalman Filter puisque l'association de données n'étant au final qu'un changement de repère, la structure de nœud ROS n'est pas adaptée.
Nous avons trouvé un PDF expliquant l'algorithme de SLAM. Grâce à celui ci nous avons déterminer les éléments à rentrer dans le noeud, ainsi que les différentes opérations incluses dans ce filtre. Pour les calculs matriciels, nous allons probablement utiliser la librairie EIGEN pour travailler sur des matrices de façon optimisée. La prochaine étape sera de "typer" nos informations (position robot + machine + murs) pour pouvoir les intégrer facilement au filtre. Nous avons aussi décidé d'inclure les murs comme landmark dans la matrice de covariance du vecteur d'état.
Il a été décidé de faire une association de données avant la détection de machines, pour distinguer les pans de murs directement afin de stocker ces informations directement à la source. On pourra éventuellement détecter les coins intérieurs de la piste pour plus de précision dans le recalage. Pour le reste, rien ne change.
Semaine 8
Localisation - Landmarks Extraction - vidéo
Pour visualiser les résultats de la détection des machines nous avons utiliser l'interface graphique disponible avec ROS, RVIZ. Nous visualisons alors le scan laser (points blancs), le résultat de la détection de segments (en rouge) et les positions des machines trouvées (en vert). Un premier test a été fait sur le scan originel, celui sur lequel nous avons travaillé depuis le début.
On rencontre un problème quand le robot est exactement parallèle ou perpendiculaire à un mur. Après vérification dans le programme, il s'avère que la détection ne fonctionne pas pour ces cas. Ce bug est maintenant corrigé :
Localisation - Data Association
La première étape consiste juste à faire un changement de repère, d'abord du repère laser vers le repère robot, puisque le laser sera placé en avant du robot, puis du repère robot au repère global, comme ci dessous :
la matrice correspondant au changement (laser -> robot) est la suivante :
0 -1 0 1 0 0.2 0 0 1
la matrice 2x2 en haut à gauche correspond à la rotation de 90°, et le vecteur (0, 0.2) correspond à la translation.
Celle du changement (robot -> global) avec alpha angle mesuré par le gyroscope depuis la position initiale (angle 0) :
cos(alpha) -sin(alpha) posInit.x
sin(alpha) cos(alpha) posInit.y
0 0 1
l'étape suivante est de vérifier si les machines vues par le laser sont bien des machines, c'est-à-dire si les positions mesurées à partir des données lasers correspond aux zones occupées par des machines envoyées par la Referee Box.
Grid Map
L'autre objectif de cette semaine a été de coder le noeud qui génère la map. La map est générée sous forme d'OccupancyGrid. Ce type est constitué d'un seul vecteur dont la première case correspond à la case en bas à gauche de la map. D'autres paramètres sont réglable comme l'origine et la taille.
Pour la taille on choisit de diviser la map en case de 10 cm et l'origine choisie est le x du centre de la map et en y l'abscisse du premier mur (voir la map ci-dessous). Afin d'expliquer comment est constituée cette map, prenons le code et analysons les différentes fonctions ainsi que le main :
Ce vecteur de Pose2D (x, y et theta (angle de la machine)) va permettre d'enregistrer la position des machines, c'est une variable global qui sera mise à jour avec le Callback :
std::vector<geometry_msgs::Pose2D> tab;
- Récupération des machines envoyées par le noeud du SLAM (sur le topic /landmarks):
void Poses_Machine_Callback(const deplacement_msg::LandmarksConstPtr &machines)
{
tab=machines->landmarks;
for (int i=0; i<tab.size(); i++)
{
tab[i].x = tab[i].x*1000;
tab[i].y = tab[i].y*1000;
}
}
- Création d'une map vide de taille 14m sur 8m. Chaque case est initialisée à une valeur nulle, on remplit également les autres paramètres de OccupancyGrid:
(On rappelle que la technique utilisée est un vecteur qui représente chaque case auxquelles il associe une probabilité 100 c'est un point interdit et 0 quand c'est un point sans danger pour le passage du robot)
void Create_Empty_Map(nav_msgs::OccupancyGrid &Map)
{
Map.info.origin.position.x=-7000;
Map.info.origin.position.y=-1000;
Map.info.origin.position.z=0;
Map.info.origin.orientation.x=0;
Map.info.origin.orientation.y=0;
Map.info.origin.orientation.z=0;
Map.info.origin.orientation.w=1;
Map.info.map_load_time=ros::Time::now();
Map.info.resolution=100;
Map.info.width=140;
Map.info.height=80;
Map.data.assign(Map.info.width*Map.info.height, 0); //map vide
}
- Construction des points fixes de la map donc les murs (probabilité 100) et les zones à risques (probabilité 50):
void Set_Wall(nav_msgs::OccupancyGrid &Map)
{
for (int i=0;i<80;i++)
{
for (int j=0;j<140;j++)
{
if ((i<13)||(i>67))) Map.data[j+i*140]=100;
if ((j<13)||(j>127)) Map.data[j+i*140]=100;
}
}
...
}
Nous ne mettons pas tout le code de cette fonction étant donné qu'il est long et répétitif puisque c'est le remplissage des données connues, donc en "dur".
- Calcul des positions machines:
Lorsqu'on reçoit une position machine, c'est en fait son centre et son orientation par rapport à x que l'on reçoit. Etant donné que les machines doivent être des rectangles de 110cm sur 75cm (réellement 70 x 35 mais on compte la moitié du robot en plus par sécurité), on décide d'abord de déterminer un des coins du rectangle et plus précisément le coin en bas à droite de ce dernier:
void Get_One_Point_Of_The_Rectangle(float x, float &xA, float y, float &yA, float theta, float largeur, float longueur)
{
float x1,y1;
x1 = x - cos(theta)*longueur;
y1 = y - sin(theta)*longueur;
xA = x1 + sin(M_PI_2-theta)*largeur;
yA = y1 - cos(M_PI_2-theta)*largeur;
}
- Remplissage des positions sur la map :
On met alors tous les points de ce rectangle à une probabilité 100 dans le vecteur Map. Pour les calculs on différencie le cas ou l'angle de la machine est entre 0 et pi/2 et le cas où il est entre pi/2 et pi. L'algorithme est le suivant :
A partir du coin, on incrémente x et y de sorte à longer le grand coté et de remplir chaque case (incrémentation de 5 cm). Une fois arrivé au bout, on incrémente x et y de 5cm sur la largeur à partir du coin et on recommence l'opération précédente. Ceci jusqu'à remplir le complètement le rectangle.
Afin d'établir les probabilités correspondantes aux cases de ce rectangle, nous utilisons la fonctions floor() pour "convertir" nos flottants en entier et accéder à la case correspondante. On notera aussi que la case 1470 correspond à l'origine de notre map.
void Set_Machines_In_Map(float rank, float theta, float xA, float yA, nav_msgs::OccupancyGrid &Map)
{
float x=xA;
float y=yA;
if (theta<=M_PI_2)
{
for (int j=0;j<10;j++)
{
for (int i=0;i<18;i++)
{
Map.data[1470+floor(x/rank)+floor(y/rank)*140]=100;
x = x + cos(theta)*50;
y = y + sin(theta)*50;
}
x = xA - j*cos(M_PI_2-theta)*50;
y = yA + j*sin(M_PI_2-theta)*50;
}
}
if (theta>M_PI_2)
{
for (int j=0;j<10;j++)
{
for (int i=0;i<18;i++)
{
Map.data[1470+floor(x/rank)+floor(y/rank)*140]=100;
x = x - sin(theta-M_PI_2)*50;
y = y + cos(theta-M_PI_2)*50;
}
x = xA - j*cos(theta-M_PI_2)*50;
y = yA - j*sin(theta-M_PI_2)*50;
}
}
}
Ci dessous on a les mains, avec les différentes fonctions appelées et la syntaxe particulière à ROS.
- Noeud général pour le traitement et le remplissage de la map :
/*========== Main ==========*/
int main(int argc, char **argv)
{
ros::init(argc, argv, "server");
ros::NodeHandle n;
ros::Subscriber sub_poses_machine = n.subscribe("/machines", 1000, Poses_Machine_Callback); // Récupération des machines
ros::Publisher Map_Pub = n.advertise<nav_msgs::OccupancyGrid>("/map", 1000); // Préparation de la publication de la map
ROS_INFO("Ready to Generate the Map");
float xA,yA;
ros::Rate loop_rate(1);
while(ros::ok())
{
nav_msgs::OccupancyGrid Map;
Create_Empty_Map(Map);
Set_Wall(Map);
for (int z=0;z<tab.size();z++)
{
Get_One_Point_Of_The_Rectangle(tab[z].x, xA, tab[z].y, yA, tab[z].theta, 275, 450);
Set_Machines_In_Map(100, tab[z].theta, xA, yA, Map);
}
Map_Pub.publish(Map); // publication de la map
ros::spinOnce();
loop_rate.sleep();
}
return 0;
}
- Noeud test qui publie 2 positions de machines :
/*========== Main ==========*/
int main(int argc, char **argv)
{
ros::init(argc, argv, "test");
ros::NodeHandle n;
ros::Publisher Pose_Machines_Pub = n.advertise<deplacement_msg::Landmarks>("/machines", 1000);
ROS_INFO("Ready to send poses machines");
int xA,yA;
ros::Rate loop_rate(1);
while(ros::ok())
{
deplacement_msg::Landmarks machines_msgs;
geometry_msgs::Pose2D tab;
tab.x=-2;
tab.y=2;
tab.theta=0;
machines_msgs.landmarks.push_back(tab);
tab.x=5;
tab.y=4;
tab.theta=2.5;
machines_msgs.landmarks.push_back(tab);
Pose_Machines_Pub.publish(machines_msgs);
ros::spinOnce();
loop_rate.sleep();
}
return 0;
}
On visualise le résultat grâce au logiciel RVIZ qui peut lire les topics publiés et donc le topic /map :
Semaine 9
Localisation - Extended Kalman Filter
l'objectif de cette semaine sera de coder toutes les fonctions nécessaires à l'implémentation finale du filtre de Kalman étendu :
- initialisations des différents éléments
- étape de prédiction
- étape de mise à jour
- publication des positions machines et du robot dans le repère global via un topic ROS
Le schéma ci-dessous nous montre les deux étapes du filtre de Kalman :
le code pour la partie prédiction :
//on ressort la position du robot pour l'état n+1
//les paramètres sont le vecteurs où on a la position du robot à l'état n, la matrice P, les commandes en vitesses et le temps à l'état n
Vector3d prediction(VectorXd xMean, MatrixXd &P, geometry_msgs::Pose2D cmdVel, ros::Time &temps){
ros::Duration duree = ros::Time::now() - temps;
double periode = duree.toSec();
Vector3d cmdVelVect = Pose2DToVector(cmdVel);
//le xMean.topLeftCorner(3,1) correspond à la position du robot
Vector3d xPredicted = xMean.topLeftCorner(3,1) + periode*cmdVelVect;
MatrixXd Fx;
Fx = MatrixXd::Identity(P.rows(), P.cols());
Fx(0,0) = xPredicted(0);
Fx(1,1) = xPredicted(1);
Fx(2,2) = xPredicted(2);
//mise à jour de P
P = Fx*P*(Fx.transpose());
//mise à jour du temps
temps = ros::Time::now();
return xPredicted;
}
le code pour la partie correction :
void correction(VectorXd &xMean, MatrixXd &P, Vector3d xPredicted, geometry_msgs::Pose2D m){
int taille = P.rows();
//on vérifie si la machine est présente ou pas dans le vecteur d'état
int i = checkStateVector(xMean, m);
if (i != 0){
//calcul de H
MatrixXd H(3, taille);
H = buildH(taille, i);
//calcul de Pm
MatrixXd Pm(taille, taille);
Pm = buildPm(P, i);
//calcul de Z
MatrixXd Z(taille, taille);
Z = H*Pm*(H.transpose());
//calcul du gain de Kalman
MatrixXd K(taille, taille);
K = P*(H.transpose())*(Z.inverse());
//mise à jour du vecteur xMean
xMean = xMean + K*(xMean.block(xMean.rows()-3,0,3,1) - xPredicted);
//mise à jour de la matrice P
P = P - K*Z*(K.transpose());
}
else {
addMachine(m, xMean, P);
}
}
Pour notre cas, on doit ajouter des nouvelles machines, alors que pour un EKF classique on observe juste des machines déjà répertoriées. Il faut donc une fonction qui permet d'ajouter une machine dans le vecteur d'état. La voilà :
void addMachine(geometry_msgs::Pose2D machine, VectorXd &xMean, MatrixXd &P){
//on redimensionne xMean et P pour accueillir la nouvelle machines
xMean.conservativeResize(xMean.rows() + 3);
P.conservativeResize(P.rows()+3,P.cols()+3);
//on remplit avec les coordonnées de la nouvelle machine
xMean(xMean.rows()-3) = machine.x;
xMean(xMean.rows()-2) = machine.y;
xMean(xMean.rows()-1) = machine.theta;
//calcul de tous les PLi
//initialisation des PLi à 0
P.block(P.rows() - 3, 0, 3, P.cols()).setZero();
P.block(0, P.cols() - 3, P.rows(), 3).setZero();
for (int j = 0; j < xMean.rows(); j = j + 3){
//position de la nouvelle machines par rapport au robot et à toutes les autres
double x = xMean(xMean.rows()-3) - xMean(j );
double y = xMean(xMean.rows()-2) - xMean(j+1);
double theta = xMean(xMean.rows()-1) - xMean(j+2);
P(P.rows()-3, j ) = x;
P(P.rows()-2, j+1) = y;
P(P.rows()-1, j+2) = theta;
P(j , P.rows()-3) = x;
P(j+1, P.rows()-2) = y;
P(j+2, P.rows()-1) = theta;
P(j , j ) = xMean(j ) - xMean(0);
P(j+1, j+1) = xMean(j+1) - xMean(1);
P(j+2, j+2) = xMean(j+2) - xMean(2);
}
}
Semaine 10
Localisation - Extended Kalman Filter
La partie prédiction du filtre marche parfaitement, quelques corrections ont dues être faites au niveau de la commande vitesse. En effet, Nous avions oublié de la transposer dans le repère global. Pour la partie correction, nous rencontrons un problème de divergence du filtre, qui est probablement due à une mauvaise initialisation. En effet, nous utilisons des enregistrements faits sur notre piste (1/4 de la vraie) avec des initialisations correspondant à la piste originale. Le filtre ne peut donc pas converger car la position de départ est fausse.
Semaine 11
Localisation - Extended Kalman Filter
Des corrections sont en cours de validation. Nous essayons de définir une initialisation avec les paramètres de notre piste, ce qui n'est pas évident. Les programmes permettant d'extraire les positions machines du filtres ont été réalisé, ainsi qu'un launch pour pouvoir lancer tous les noeuds de la localisation.
Semaine 12
Compétition Open German - mise en place
Pendant les deux jours de mise en place, nous avons continué à travailler sur la localisation, qui est une partie critique et nécessaire à notre participation. Le filtre en lui même est fonctionnel et permet de corriger la position du robot, ainsi que celle des machines. Cependant, et ce n'est pas un petit "cependant"... Le fait que l'on ajoute des machines en cours de jeu perturbe fortement notre algorithme.
En effet, le filtre de Kalman est optimal si la position des repères est connu, or, un ajout de machine crée un recalage forcé, et si l'on voit plusieurs machines... C'est la catastrophe. L'ajout de machines est une partie sensible qui nécessite des tests sur la position mesurée, avec un changement de repère à partir de la position du robot, si celle ci dérive, tout dérive. Chaque machine initialisée à la mauvaise position, ou chaque élément détecté comme machine mais n'en étant pas une (faux positif) perturbe le recalage.
De nombreux tests ayant été fait sur la piste officiel avec différentes configurations nous ont permis de vérifier que l'odométrie mesurée ne dérivait que très peu. Il a donc été décidé de n'utiliser que l'odométrie et le scan laser pour la partie exploration. En effet, chaque machine mesurée est envoyée à un noeud ROS qui va créer une carte et la compléter au fur et à mesure de la partie. Le robot est donc repéré rien qu'avec son odométrie. Le fait que la phase d'exploration (découverte du terrain) ne dure que 4 minutes nous a convaincu pour n'utiliser que cette mesure.
De plus, la carte créée sera utilisée pour la phase suivante, la phase de production. Cette phase consiste, au niveau de la localisation, à se repérer sur la piste et atteindre la machine demandée par l'exécuteur de tâches. Pour cette phase qui dure 15 minutes, l'utilisation du filtre est nécessaire. Donc, avec les coordonnées des machines mesurées pendant la première phase, on peut créer le vecteur d'état et la matrice faisant le lien entre les machines. De là, la taille de ces deux éléments ne variant plus, on peut corriger uniquement la position du robot et le filtre sera efficace.
Compétition Open German - 1er jour
Durant ce premier jour, nous avons commencé à merger nos branches respectives pour pouvoir faire tourner tous nos programmes. Cette phase est laborieuse et nous a pris du temps. De toute façon, toutes les équipes ne sont pas prêtes, les organisateurs non plus. La Referee Box n'est pas fonctionnel pour la phase de production, ce qui veut dire que nous nous concentrons actuellement sur l'exploration. Les matchs joués aujourd'hui ne nous rapporte donc pas de points. Les tests nous ont permis de valider individuellement chacun des algos, il ne reste "plus qu'à" rejoindre le tout.
Compétition Open German - 2eme jour
Niveau localisation, la navigation à l'odométrie et la détection de machine sont fonctionnelles. Cependant, le moyennage fait sur les positions machines (on moyenne toutes les positions trouvées appartenant à une même machine pour n'avoir qu'un seul point) fait que le point correspondant peut être perturbé par des mesures aberrantes. C'est le cas lorsque le robot se déplace à vitesse élevée.
La détection de machine a été améliorée afin de ne rajouter QUE les machines, et pas les murs de la même taille. Nous allons donc retester le filtre de Kalman Etendu avec cette amélioration. Cependant, ce ne sera fait qu'après la compétition, puisque d'autres problèmes ont nécessité la présence de l'équipe sur certaines parties sensibles du déplacement.
Sur la piste nous avons fait des mesures, qui nous donnent la carte suivante :
La visualisation du trajet pour découvrir ces machines est le suivant :
Et les positions machines, ainsi que leur orientation sont les suivantes :
Compétition Open German - 3eme et dernier jour
L'architecture choisie pour la localisation est la suivante :
- Navigation à l'odométrie
- Détection de machines et moyennage
- Quand on a vu toutes nos machines, on utilise la symétrie pour compléter les machines restantes
- Navigation et Localisation avec l'EKF (correction des positions machines et du robot)
Localisation - Extended Kalman Filter
Après de longs tests et des corrections importantes au niveau de l'ajout des machines dans le filtre, ce qui était la partie critique... Le meilleur résultat que l'on ait pu avoir avec l'EKF est celui ci dessous. Les machines étant en violet, la trajectoire calculée par l'EKF en vert et la trajectoire mesurée par les codeurs en rouge.
Nous rappelons que tous nos codes sont disponibles sur notre GIT.
Video
Enfin, afin d'illustrer nos résultats de manière ludique et attrayante, voici une vidéo qui vous donnera goût à la RoboCup !