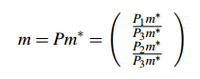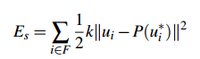InitRech 2015/2016, sujet 5 : Différence entre versions
(Page créée avec « = Summary = = Applications = ») |
(→Summary) |
||
| Ligne 1 : | Ligne 1 : | ||
= Summary = | = Summary = | ||
| + | |||
| + | With the technology such as augmented reality, researcher are confronted against new problem like image processing, facial recognition system and 3D shape recovery. | ||
| + | this paper show a newer method in real time to calculate a 3D deformable shape with a monocular video sequence. | ||
| + | Firstly authors explain what is the context and what did we wonder to resolve this subject. Next, they describe algorithms already use in 3D recovery for non rigid shape and their assets of this 4 four technologies : | ||
| + | ** Mechanical models | ||
| + | ** Mass-spring systems | ||
| + | ** Learned non-rigid models | ||
| + | ** Parametric models | ||
| + | In addition historic of previous research and their contribution are given in term of efficiency to compute image processing and to recover a 3D elastic shape with one point of view. | ||
| + | After many assumption they succeed to minimize in a non-linear problem for non-rigid shape, result this equation: | ||
| + | [[Fichier:Matriceformule.png|200px|thumb|center|]] | ||
| + | Knowing that, m is a point of our image m = (x,y), P* the matrix projection of the view and m* is the projection of the point (x*,y*,z*) in our image. | ||
| + | Thanks to energy equation to characterize the 3D deformation: | ||
| + | [[Fichier:Energy.png|200px|thumb|center|]] | ||
| + | They resolve this problem as an energy minimization problem accounting for a non-linear elastic model constrains to a static view with the knowledge of his matrice projection. To continue they use tool like Gauss Seidel and Euler to solve this problem on compute. | ||
| + | In the last part they describe tests and compare to algorithm already existing and what is the process to solve self-occlusion handling. | ||
= Applications = | = Applications = | ||
Version du 18 juin 2016 à 18:49
Summary
With the technology such as augmented reality, researcher are confronted against new problem like image processing, facial recognition system and 3D shape recovery. this paper show a newer method in real time to calculate a 3D deformable shape with a monocular video sequence. Firstly authors explain what is the context and what did we wonder to resolve this subject. Next, they describe algorithms already use in 3D recovery for non rigid shape and their assets of this 4 four technologies :
- Mechanical models
- Mass-spring systems
- Learned non-rigid models
- Parametric models
In addition historic of previous research and their contribution are given in term of efficiency to compute image processing and to recover a 3D elastic shape with one point of view. After many assumption they succeed to minimize in a non-linear problem for non-rigid shape, result this equation:
Knowing that, m is a point of our image m = (x,y), P* the matrix projection of the view and m* is the projection of the point (x*,y*,z*) in our image. Thanks to energy equation to characterize the 3D deformation:
They resolve this problem as an energy minimization problem accounting for a non-linear elastic model constrains to a static view with the knowledge of his matrice projection. To continue they use tool like Gauss Seidel and Euler to solve this problem on compute. In the last part they describe tests and compare to algorithm already existing and what is the process to solve self-occlusion handling.