Réalité Augmentée pour la chirurgie : Différence entre versions
(→Deuxième partie) |
(→Conclusion) |
||
| (28 révisions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 78 : | Ligne 78 : | ||
Les VBO permettent de gagner un temps considérable à OpenGL en évitant de faire des aller-retours inutiles entre la RAM et la mémoire graphique: | Les VBO permettent de gagner un temps considérable à OpenGL en évitant de faire des aller-retours inutiles entre la RAM et la mémoire graphique: | ||
| − | [[Fichier:interet_VBO.png]] | + | [[Fichier:interet_VBO.png|400px|thumb|center]] |
| − | [[Fichier:chargement_avec_VBO.png]] | + | [[Fichier:chargement_avec_VBO.png|400px|thumb|center]] |
| − | [[Fichier:affichage_avec_VBO.png]] | + | [[Fichier:affichage_avec_VBO.png|400px|thumb|center]] |
Images prises sur : http://fr.openclassrooms.com/informatique/cours/developpez-vos-applications-3d-avec-opengl-3-3/c-est-quoi-un-vbo | Images prises sur : http://fr.openclassrooms.com/informatique/cours/developpez-vos-applications-3d-avec-opengl-3-3/c-est-quoi-un-vbo | ||
| Ligne 98 : | Ligne 98 : | ||
Rédaction du rapport d'avancement | Rédaction du rapport d'avancement | ||
| − | Rédaction de la présentation | + | Rédaction de la présentation orale |
= Conclusion Première partie = | = Conclusion Première partie = | ||
| Ligne 119 : | Ligne 119 : | ||
-Résoudre le problème d'affichage du foie grâce aux VBO | -Résoudre le problème d'affichage du foie grâce aux VBO | ||
| + | |||
-Finir l'implémentation du calcul de distances | -Finir l'implémentation du calcul de distances | ||
| + | |||
-Réaliser des propositions d'affichage des distances | -Réaliser des propositions d'affichage des distances | ||
| − | |||
== Semaine 1 == | == Semaine 1 == | ||
| Ligne 133 : | Ligne 134 : | ||
nous allons changer l'affichage du foie de tel sorte que l'on voit que les traits reliant les triangles sans couleur ni texture. | nous allons changer l'affichage du foie de tel sorte que l'on voit que les traits reliant les triangles sans couleur ni texture. | ||
On affiche désormais le foie et la tumeur ensemble avec pour le foie juste des traits pour avoir une meilleure vision de la position de la tumeur. | On affiche désormais le foie et la tumeur ensemble avec pour le foie juste des traits pour avoir une meilleure vision de la position de la tumeur. | ||
| + | [[Fichier:tumeur_foie.jpg|400px|thumb|center|Affichage de la tumeur et du foie]] | ||
| + | [[Fichier:tumeur_foie_zoom.png|400px|thumb|center|A l'intérieur du foie]] | ||
| + | On voit en marron la tumeur et en rose le foie. | ||
== Semaine 3 == | == Semaine 3 == | ||
| Ligne 140 : | Ligne 144 : | ||
Ce calcul se réalise en plusieurs étapes mathématiques présentées ci dessous : | Ce calcul se réalise en plusieurs étapes mathématiques présentées ci dessous : | ||
| − | + | ::[[Fichier:Raytracing.png|400px|thumb|center]] | |
Afin de savoir s’il y a intersection entre un rayon et un triangle, il est plus aisé de commencer tout d’abord par vérifier s’il y a intersection entre ce même rayon et le plan contenant le triangle. | Afin de savoir s’il y a intersection entre un rayon et un triangle, il est plus aisé de commencer tout d’abord par vérifier s’il y a intersection entre ce même rayon et le plan contenant le triangle. | ||
Pour cela, on calcule le vecteur normal du plan. Le vecteur normal du plan s’obtient en faisant le produit vectoriel de deux vecteurs non colinéaires du plan. On connaît 3 points du plan (les points constituant le triangle en train d’être testé), que l’on nommera ici v0, v1 et v2. On peut donc calculer le produit vectoriel de v0v1 et v0v2 par exemple, pour obtenir le vecteur normal N(A,B,C). Une fois le vecteur normal obtenu, on réalise le produit scalaire entre N et le rayon. Si le résultat est nul, le plan et le rayon sont parallèles donc il n’y a pas intersection. Sinon on a confirmation que le rayon et le plan entrent en intersection. | Pour cela, on calcule le vecteur normal du plan. Le vecteur normal du plan s’obtient en faisant le produit vectoriel de deux vecteurs non colinéaires du plan. On connaît 3 points du plan (les points constituant le triangle en train d’être testé), que l’on nommera ici v0, v1 et v2. On peut donc calculer le produit vectoriel de v0v1 et v0v2 par exemple, pour obtenir le vecteur normal N(A,B,C). Une fois le vecteur normal obtenu, on réalise le produit scalaire entre N et le rayon. Si le résultat est nul, le plan et le rayon sont parallèles donc il n’y a pas intersection. Sinon on a confirmation que le rayon et le plan entrent en intersection. | ||
| + | |||
Cela permet ensuite, si intersection il y a, de calculer les coordonnées du point d’intersection P entre le rayon et le plan. P est défini de cette façon: | Cela permet ensuite, si intersection il y a, de calculer les coordonnées du point d’intersection P entre le rayon et le plan. P est défini de cette façon: | ||
| − | P = O + t * D | + | |
| − | + | P = O + t * D | |
| − | + | :::-O l’origine (ici le barycentre de la tumeur) | |
| + | :::-D le vecteur directeur du rayon | ||
| + | :::-t la distance entre O et P | ||
| Ligne 154 : | Ligne 161 : | ||
L’équation du plan contenant le triangle est celle-ci: | L’équation du plan contenant le triangle est celle-ci: | ||
| − | A * x + B * y + C * z + d = 0 | + | |
| − | plan N(A,B,C). | + | A * x + B * y + C * z + d = 0 |
| − | -(x,y,z) un point du plan. | + | :::-A,B et C sont les composantes du vecteur normal au |
| − | -d la distance de l’origine (du repère) au plan, suivant la direction du vecteur normal au plan. | + | :::plan N(A,B,C). |
| + | :::-(x,y,z) un point du plan. | ||
| + | :::-d la distance de l’origine (du repère) au plan, suivant la direction du vecteur normal au plan. | ||
| + | |||
Grâce aux deux formules précedentes, on en déduit le calcul de t : | Grâce aux deux formules précedentes, on en déduit le calcul de t : | ||
| + | |||
t = - ( N . O + d ) / ( N . D) | t = - ( N . O + d ) / ( N . D) | ||
| + | |||
Une fois t calculé, on peut aisément obtenir les coordonnées de P. On peut maintenant passer au deuxième test à réaliser, qui est le test d’appartenance d’un point à un triangle. | Une fois t calculé, on peut aisément obtenir les coordonnées de P. On peut maintenant passer au deuxième test à réaliser, qui est le test d’appartenance d’un point à un triangle. | ||
| Ligne 169 : | Ligne 181 : | ||
| − | [[Fichier:Raytracing1.png]] | + | ::[[Fichier:Raytracing1.png|400px|thumb|center]] |
| Ligne 178 : | Ligne 190 : | ||
Le principe de ce test est le suivant: | Le principe de ce test est le suivant: | ||
| + | |||
On calcule les vecteurs partant des points du triangle et allant vers P : v0P, v1P, v2P. | On calcule les vecteurs partant des points du triangle et allant vers P : v0P, v1P, v2P. | ||
| + | |||
On calcule de même les vecteurs correspondants aux cotés du triangle : v0v1, v1v2, v2v0. | On calcule de même les vecteurs correspondants aux cotés du triangle : v0v1, v1v2, v2v0. | ||
| + | |||
On calcule le produit vectoriel de chacun de ces vecteurs avec les vecteurs contenant P: | On calcule le produit vectoriel de chacun de ces vecteurs avec les vecteurs contenant P: | ||
| + | |||
u = v0v1 ^ v0P, v = v1v2 ^ v1P, w = v2v0 ^ v2P. | u = v0v1 ^ v0P, v = v1v2 ^ v1P, w = v2v0 ^ v2P. | ||
| + | |||
Si P appartient au triangle, les vecteurs u, v et w ainsi calculés seront colinéaires de même sens avec le vecteur normal au triangle N. (voir Figure 11) | Si P appartient au triangle, les vecteurs u, v et w ainsi calculés seront colinéaires de même sens avec le vecteur normal au triangle N. (voir Figure 11) | ||
On réalise donc les tests suivants: (produit scalaire) | On réalise donc les tests suivants: (produit scalaire) | ||
| + | |||
N . u, N . v, N . w | N . u, N . v, N . w | ||
| Ligne 195 : | Ligne 213 : | ||
| − | [[Fichier:Raytracing2.png]] | + | ::[[Fichier:Raytracing2.png|400px|thumb|center]] |
| Ligne 202 : | Ligne 220 : | ||
Une fois ces tests concluants, on récupère la distance voulue avec le calcul suivant : | Une fois ces tests concluants, on récupère la distance voulue avec le calcul suivant : | ||
| + | |||
Distance = t * D(x,y,z) | Distance = t * D(x,y,z) | ||
| + | |||
Ceci nous donne une distance selon les 3 axes, grâce à une comparaison du vecteur directeur et des vecteurs X, Y, et Z, on récupère uniquement la distance voulue : | Ceci nous donne une distance selon les 3 axes, grâce à une comparaison du vecteur directeur et des vecteurs X, Y, et Z, on récupère uniquement la distance voulue : | ||
| + | |||
Distance = t * D.x ou t * D.y ou t *D.z | Distance = t * D.x ou t * D.y ou t *D.z | ||
| Ligne 210 : | Ligne 231 : | ||
== Semaine 4 == | == Semaine 4 == | ||
| + | |||
| + | |||
| + | Diagramme UML de notre application finale: | ||
| + | |||
| + | |||
| + | [[Fichier:UML.PNG|600px|thumb|center]] | ||
| + | |||
| + | |||
| + | Voici un bref résumé de chacune des classes et de leurs fonctions : | ||
| + | |||
| + | La classe Camera.cpp s’occupe de gérer tous les placements et les orientations que la caméra va prendre. | ||
| + | |||
| + | La classe Input.cpp s’occupe de gérer tous les évènements clavier et souris, les rendant plus simples d’utilisation. | ||
| + | |||
| + | La classe Shader.cpp permet de charger et de compiler le shader en charge de l’affichage de couleurs sur notre représentation. | ||
| + | |||
| + | La classe principale: SceneOpenGL.cpp qui met en relation les différentes classes, permet la création de la scène, et dans laquelle nous avons codé les différentes fonctions nécessaires au programme, notamment la fonction de calcul des distances. | ||
| + | |||
| + | La classe Texture.cpp permet de charger des textures à la place des couleurs. | ||
| + | |||
| + | La classe Tumor.cpp permet de récupérer les vertices de la tumeur et de l’afficher. | ||
| + | |||
| + | La classe Liver.cpp permet de récupérer les vertices du foie et de l’afficher. | ||
| + | |||
| + | La classe DistanceDisplay.cpp permet d’afficher les distances séparant la tumeur de la surface du foie suivant les trois axes x, y et z. | ||
| + | |||
| + | On a fait quelques propositions d'affichage pour les distances entre la tumeur et le foie suivant les trois axes : | ||
| + | |||
| + | [[Fichier:affichage_point_intersection.jpg|400px|thumb|center|Affichage des points d'intersection]] | ||
| + | [[Fichier:Affichage_en_ligne.jpg|400px|thumb|center|Affichage en ligne]] | ||
| + | [[Fichier:Affichage_avec_des_cylindres.jpg|400px|thumb|center|Affichage avec des cylindres]] | ||
| + | [[Fichier:Affichage_avec_des_cones.jpg|400px|thumb|center|Affichage avec des cônes]] | ||
| + | |||
| + | Il faut noter que la décision qu'en à quelle afifchage utiliser au final ne nous appartient pas. Ces propositions seront proposées aux chirurgiens qui décideront de la quelle prendre ou améliorer ou encore en faire une nouvelle. | ||
= Conclusion = | = Conclusion = | ||
| + | |||
| + | Ce projet nous a permis d’apporter notre contribution dans un domaine concret et important qu’est la médecine. De même, il nous a permis d’appréhender les techniques de modélisation utilisées de nos jours avec OpenGL. | ||
| + | Du point de vue réalisation, notre application affiche la tumeur et le foie en 3 dimensions et permet aussi de visualiser les distances, suivant les trois axes (x, y et z ), entre la tumeur et la surface du foie. Différentes solutions de représentation de ces distances ont été proposées et laissées à l’appréciation des chirurgiens, à qui appartiendra la décision finale sur l’utilité et la lisibilité de chacune d’entre-elles, ainsi décideront-ils d’en garder une ou plusieurs, d’en améliorer une autre, ou peut-être que nos propositions ne leur conviendront pas, mais elles auront au moins permis de donner des pistes à l’équipe de recherche Shacra pour la suite de ses travaux. | ||
| + | |||
| + | |||
| + | [[Fichier:Rapport_realite_augmentee.pdf]] | ||
Version actuelle datée du 28 février 2014 à 16:56
Papa Momar MBOUP/ Calvin DELBERGHE
Sommaire
Présentation
Description et Objectif:
Notre projet consiste à assister les chirurgiens lors de chirurgies laparoscopiques. La chirurgie laparoscopique est une technique chirurgicale minimalement invasive où le chirurgien réalise une opération de l'abdomen par de petites incisions où sont placés des trocars qui permettent le passage de fins instruments chirurgicaux. Dans le cadre de ce projet, il s’agit de réaliser l’ablation de la(des) tumeur(s) présente(s) dans le foie du patient. La localisation des tumeurs ainsi que de l’ensemble du réseau vasculaire peut etre réalisé grâce à un scanner pré-opératoire et donc reconstruits en 3D. Cependant, ils ne peuvent pas être visualisés par la caméra lors de l’opération chirurgicale.
Ainsi, le chirurgien ne peut en aucun cas connaitre la localisation de la tumeur et ne peut pas se représenter la distance qui la sépare des parois du foie. D’où le but de notre projet: aider les chirurgiens dans ces opérations. Des travaux récents de l'équipe de recherche Shacra ont permis de suivre avec une bonne précision le mouvement de structures internes du foie pendant une opération laparoscopique. Le projet consiste à utiliser ces travaux pour mélanger le flux vidéo fourni par l'endoscope aux informations calculées par la simulation pour fournir aux chirurgiens des informations utiles sur la position des structures internes du foie lors de la manipulation. Différentes pistes pourront être explorées pour ne pas surcharger le flux vidéo tout en fournissant les informations importantes (position, profondeur, distance à la surface du foie...)
Environnement de travail :
1 ordinateur
OpenGL 3.3
SDL 2.0
IDE CodeBlocks
Plan d'action / Gestion de projet
Dans un premier temps, nous allons commencer à suivre des tutoriaux sur le framework OpenGL. Quand on sera assez avancé, nous débuterons le codage du programme principal. Donc pour le premier semestre, le plan est de mettre en place la base du programme et de bien maîtriser OpenGL pour la suite quand on ajoutera des fonctions plus poussées dans le programme.
Réalisation
Semaine 37
Présentation et Choix du sujet.
Semaine 38
Rencontre avec les encadrants du projet:
Explication détaillée du sujet ainsi que les attentes du projet. Réception des premières données pour débuter quelques tests avec OpenGL.
Semaine 39
Installation d'OpenGL sous Windows avec CodeBlocks. Début des tutoriaux sur le site du zéro:
http://fr.openclassrooms.com/informatique/cours/developpez-vos-applications-3d-avec-opengl-3-3
Semaine 40
Poursuite des tutoriaux.
Semaine 41
Poursuite des tutoriaux.
Semaine 42
Poursuite des tutoriaux.
Semaine 43
Poursuite des tutoriaux
Semaine 44
Poursuite des tutoriaux
Semaine 45
Poursuite des tutoriaux
Semaine 46
Poursuite des tutoriaux
Semaine 47
Fin de la première partie des tutoriaux.
Semaine 48
Démarrage du code du programme à partir du code réalisé pendant les tutoriels.
Semaine 49
Ajout de la fonction permettant de récupérer les données des fichiers .obj contenant les vertices, les coordonnées de texture, les vecteurs normaux et les références aux faces (triangles) constituant l'objet 3D.
Semaine 50
Nous sommes arrivé durant cette semaine à représenter une tumeur correctement en 3D.
Pour représenter un structure en 3D, nous allons utiliser un ensemble de triangle. Chaque triangle est constitué de 3 vertices qui sont ces sommets. Un vertex est tout simplement un point avec trois dimensions : x,y et z. Ainsi, le but est de relier les trois sommets (vertices) formant un triangle et ensuite de relier tous les triangles. Ainsi, nous obtiendront notre structure en 3D.
Cependant, nous rencontrons un problème quand on a un nombre de vertices élevés à représenter (de l'ordre de 20000 vertices). Une des pistes pour la résolution de ce problème est d'utiliser les display list. Cependant, les display List n'existent plus en OpenGL 3.3. Donc le problème reste irrésolu pour l'instant. On va regarder du coté des VBO (Vertex Buffer Object) et VBA(Vertex Buffer Array).
Les "Display List" permettent un stockage des données sur la carte graphique mais ne permettent pas de mettre à jour ces données. Les "VertexArray" conservent les données dans des tampons en mémoire système ce qui permet de les modifier mais oblige à transférer toutes ces données à chaque fois qu'elles doivent être affichées.
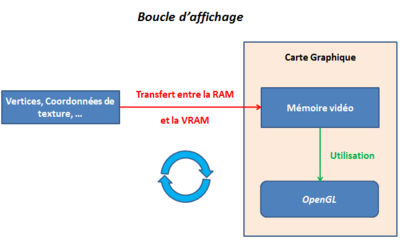
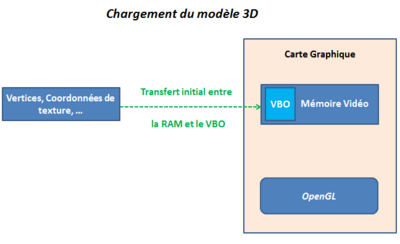
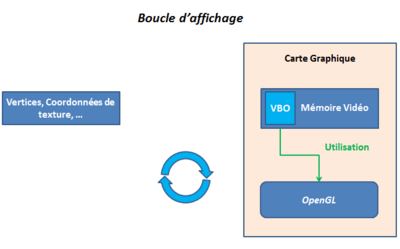
Un VBO est un objet OpenGL qui contient des données relatives à un modèle 3D comme les vertices, les coordonnées de texture, les normales (pour les lumières), ... Sa particularité vient du fait que les données qu'il contient se trouvent non pas dans la RAM mais directement dans la carte graphique.
Les VBO permettent de gagner un temps considérable à OpenGL en évitant de faire des aller-retours inutiles entre la RAM et la mémoire graphique:
Images prises sur : http://fr.openclassrooms.com/informatique/cours/developpez-vos-applications-3d-avec-opengl-3-3/c-est-quoi-un-vbo
On économise ainsi le transfert de centaines de milliers de données à chaque affichage, la carte graphique peut travailler plus rapidement.
Nous avons aussi trouvé durant cette semaine ce site qui explique très bien la théorie de l'intersection rayon/triangle avec une traduction en code.
Nous avons grâce à ceci pu coder une méthode adaptée pour tester les triangles de la surface du foie et voir s'ils sont en intersection avec le rayon partant du barycentre de la tumeur et ayant pour vecteur directeur X, Y, ou Z. Une fois le bon triangle trouvé, la fonction se charge de renvoyer le point d'intersection, et il ne reste qu'a récupérer sa coordonnée en X,Y,ou Z (suivant le vecteur directeur précisé dans l'appel à la fonction) qui se trouve être la distance entre la tumeur et la surface du foie. Pour affiner un peu notre méthode, il faut d'abord l'appliquer à l'enveloppe de la tumeur elle même, puis faire de même avec la surface du foie, et soustraire les coordonnées obtenues pour les points d'intersections dans chacune des 3 direction afin d'obtenir une distance correcte pour chaque direction.
Semaine 51
Rédaction du rapport d'avancement
Rédaction de la présentation orale
Conclusion Première partie
Ce premier semestre à travailler sur ce projet a été des plus instructifs pour nous, nous permettant de mieux concevoir la charge de travail que représentait celuici, de réaliser la chance qu’il nous était donnée de pouvoir apporter notre contribution dans le domaine concret et important qu’est la médecine. Cela nous aura aussi permis de nous cultiver sur les méthodes utilisées aujourd’hui en chirurgie, ainsi que de découvrir OpenGL et la modélisation dans l’espace. Les bases de l’application sont bien en place et le cahier des charges bien défini. Il reste donc pour la seconde moitié de l’année à finaliser la modélisation des structures ainsi que l’affichage de la distance entre la tumeur et la surface du foie. De plus, nous devrons rendre l’application dynamique avec la récupération des flux de données en temps réel par la caméra.
Deuxième partie
Objectifs
-Résoudre le problème d'affichage du foie grâce aux VBO
-Finir l'implémentation du calcul de distances
-Réaliser des propositions d'affichage des distances
Semaine 1
Nous avons créé une classe foie pour représenter ce dernier. De ce fait, notre programme sera plus lisible et ordonné.
Semaine 2
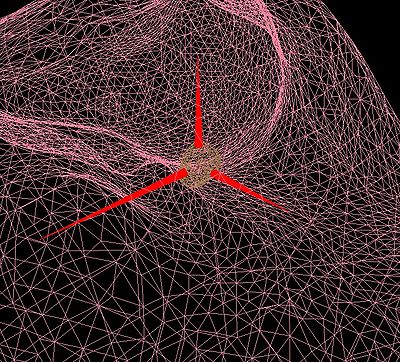
On arrive enfin à représenter le foie. Pour celà donc, nous avons utilisé les VBO afin d'aboutir à ce résultat. La prochaine étape est de représenter la tumeur et le foie en même temps. Nous avons créé une classe tumeur qui s'occupe du chargement et de l'affichage de la tumeur. Nous arrivons maintenant à afficher le foie et la tumeur en même temps. Cependant, vu que la tumeur se trouve à l'intérieur du foie, nous allons changer l'affichage du foie de tel sorte que l'on voit que les traits reliant les triangles sans couleur ni texture. On affiche désormais le foie et la tumeur ensemble avec pour le foie juste des traits pour avoir une meilleure vision de la position de la tumeur.
On voit en marron la tumeur et en rose le foie.
Semaine 3
Pour cette semaine, nous sommes arrivés à calculer les distances séparant la tumeur et la surface du foie.
Afin de récupérer la distance séparant la tumeur et le foie, on réalise des tests d’intersection rayon-triangle avec les triangles composant les meshs du foie et de la tumeur. En effet, en réalisant ce test entre un rayon partant du barycentre de la tumeur suivant la direction X,Y ou Z, et les triangles constituant le foie d’une part, et la tumeur d’autre part, on obtient deux distances (toujours selon X, Y, ou Z). La première, distance entre la paroi du foie et le barycentre de la tumeur, la seconde, distance entre la paroi de la tumeur et le barycentre de celle ci. En soustrayant la seconde à la première, on obtient la distance séparant la paroi du foie et la paroi de la tumeur selon un axe prédéfini (X, Y ou Z de notre repère). Il suffit ensuite de réaliser le calcul une fois pour chaque axe. Ce calcul se réalise en plusieurs étapes mathématiques présentées ci dessous :
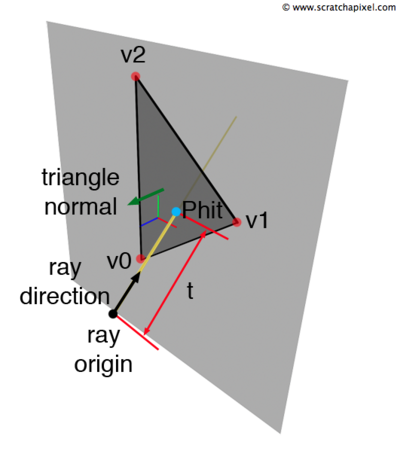
Afin de savoir s’il y a intersection entre un rayon et un triangle, il est plus aisé de commencer tout d’abord par vérifier s’il y a intersection entre ce même rayon et le plan contenant le triangle.
Pour cela, on calcule le vecteur normal du plan. Le vecteur normal du plan s’obtient en faisant le produit vectoriel de deux vecteurs non colinéaires du plan. On connaît 3 points du plan (les points constituant le triangle en train d’être testé), que l’on nommera ici v0, v1 et v2. On peut donc calculer le produit vectoriel de v0v1 et v0v2 par exemple, pour obtenir le vecteur normal N(A,B,C). Une fois le vecteur normal obtenu, on réalise le produit scalaire entre N et le rayon. Si le résultat est nul, le plan et le rayon sont parallèles donc il n’y a pas intersection. Sinon on a confirmation que le rayon et le plan entrent en intersection.
Cela permet ensuite, si intersection il y a, de calculer les coordonnées du point d’intersection P entre le rayon et le plan. P est défini de cette façon:
P = O + t * D
- -O l’origine (ici le barycentre de la tumeur)
- -D le vecteur directeur du rayon
- -t la distance entre O et P
L’équation du plan contenant le triangle est celle-ci:
A * x + B * y + C * z + d = 0
- -A,B et C sont les composantes du vecteur normal au
- plan N(A,B,C).
- -(x,y,z) un point du plan.
- -d la distance de l’origine (du repère) au plan, suivant la direction du vecteur normal au plan.
Grâce aux deux formules précedentes, on en déduit le calcul de t :
t = - ( N . O + d ) / ( N . D)
Une fois t calculé, on peut aisément obtenir les coordonnées de P. On peut maintenant passer au deuxième test à réaliser, qui est le test d’appartenance d’un point à un triangle.
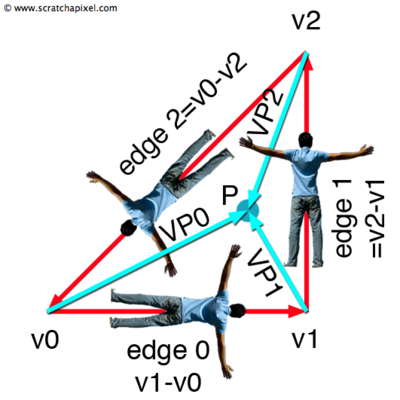
Le principe de ce test est le suivant:
On calcule les vecteurs partant des points du triangle et allant vers P : v0P, v1P, v2P.
On calcule de même les vecteurs correspondants aux cotés du triangle : v0v1, v1v2, v2v0.
On calcule le produit vectoriel de chacun de ces vecteurs avec les vecteurs contenant P:
u = v0v1 ^ v0P, v = v1v2 ^ v1P, w = v2v0 ^ v2P.
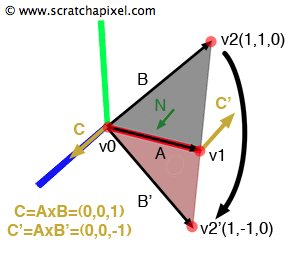
Si P appartient au triangle, les vecteurs u, v et w ainsi calculés seront colinéaires de même sens avec le vecteur normal au triangle N. (voir Figure 11)
On réalise donc les tests suivants: (produit scalaire)
N . u, N . v, N . w
Si le résultat est positif, P est placé à l’intérieur du triangle par rapport au coté testé. (u teste le coté v0v1, v teste v1v2, w teste v2v0) Si les trois tests sont positifs, cela signifie que P est bien à l’intérieur du triangle.
Une fois ces tests concluants, on récupère la distance voulue avec le calcul suivant :
Distance = t * D(x,y,z)
Ceci nous donne une distance selon les 3 axes, grâce à une comparaison du vecteur directeur et des vecteurs X, Y, et Z, on récupère uniquement la distance voulue :
Distance = t * D.x ou t * D.y ou t *D.z
Pour le temps restant au projet, nous allons proposer différentes solutions pour l'affichage de ces distances. De même, nous allons rédiger notre rapport et nous préparer à la soutenance finale.
Semaine 4
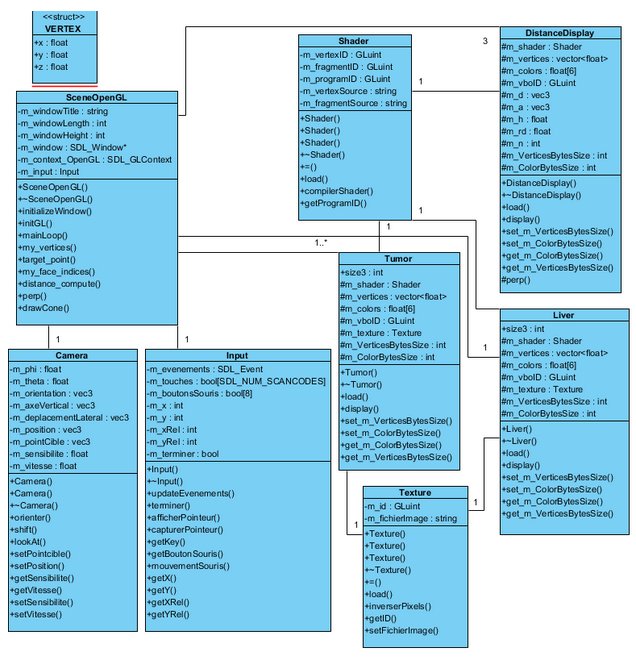
Diagramme UML de notre application finale:
Voici un bref résumé de chacune des classes et de leurs fonctions :
La classe Camera.cpp s’occupe de gérer tous les placements et les orientations que la caméra va prendre.
La classe Input.cpp s’occupe de gérer tous les évènements clavier et souris, les rendant plus simples d’utilisation.
La classe Shader.cpp permet de charger et de compiler le shader en charge de l’affichage de couleurs sur notre représentation.
La classe principale: SceneOpenGL.cpp qui met en relation les différentes classes, permet la création de la scène, et dans laquelle nous avons codé les différentes fonctions nécessaires au programme, notamment la fonction de calcul des distances.
La classe Texture.cpp permet de charger des textures à la place des couleurs.
La classe Tumor.cpp permet de récupérer les vertices de la tumeur et de l’afficher.
La classe Liver.cpp permet de récupérer les vertices du foie et de l’afficher.
La classe DistanceDisplay.cpp permet d’afficher les distances séparant la tumeur de la surface du foie suivant les trois axes x, y et z.
On a fait quelques propositions d'affichage pour les distances entre la tumeur et le foie suivant les trois axes :
Il faut noter que la décision qu'en à quelle afifchage utiliser au final ne nous appartient pas. Ces propositions seront proposées aux chirurgiens qui décideront de la quelle prendre ou améliorer ou encore en faire une nouvelle.
Conclusion
Ce projet nous a permis d’apporter notre contribution dans un domaine concret et important qu’est la médecine. De même, il nous a permis d’appréhender les techniques de modélisation utilisées de nos jours avec OpenGL. Du point de vue réalisation, notre application affiche la tumeur et le foie en 3 dimensions et permet aussi de visualiser les distances, suivant les trois axes (x, y et z ), entre la tumeur et la surface du foie. Différentes solutions de représentation de ces distances ont été proposées et laissées à l’appréciation des chirurgiens, à qui appartiendra la décision finale sur l’utilité et la lisibilité de chacune d’entre-elles, ainsi décideront-ils d’en garder une ou plusieurs, d’en améliorer une autre, ou peut-être que nos propositions ne leur conviendront pas, mais elles auront au moins permis de donner des pistes à l’équipe de recherche Shacra pour la suite de ses travaux.