Version du 10 février 2014 à 15:39 (voir la source) Mlenorma (discussion | contributions) (→‎Semaines de modules transversaux : du 6 au 10 Janvier 2014, du 13 au 17 Janvier 2014, du 20 au 24 Janvier 2014) ← Modification précédente		Version actuelle datée du 26 juin 2014 à 16:03 (voir la source) Tvantroy (discussion | contributions)
(96 révisions intermédiaires par un autre utilisateur non affichées)
Ligne 1 :		Ligne 1 :
		+
		+
		+	<include nopre noesc src="/home/pedago/pimasc/include/video-LocalisationRobot-iframe.html" />
		+
	= Présentation du Robotino =		= Présentation du Robotino =
Ligne 84 :		Ligne 88 :
	- Un gyroscope		- Un gyroscope
−	Un nouveau capteur	+	Un nouveau capteur :
	- Un module Northstar		- Un module Northstar
Ligne 532 :		Ligne 536 :
	Compilation du programme Matlab nommé '''Northstar.m''', 2 messages d'erreurs :		Compilation du programme Matlab nommé '''Northstar.m''', 2 messages d'erreurs :
−	Error using ==> loadlibrary at 282	+	Error using ==> loadlibrary at 282
		+	Microsoft Visual C++ 2005 or 2008 is required to use this feature.
−	Microsoft Visual C++ 2005 or 2008 is required to use this feature.	+	Error in ==> init at 20
−		+	loadlibrary( 'rec_robotino_com_c.dll', 'Com.h')
−	Error in ==> init at 20
−
−	loadlibrary( 'rec_robotino_com_c.dll', 'Com.h')
	La première erreur est dû à la version de Microsoft Visual C++.		La première erreur est dû à la version de Microsoft Visual C++.
Ligne 560 :		Ligne 562 :
	== Semaines de modules transversaux : du 6 au 10 Janvier 2014, du 13 au 17 Janvier 2014, du 20 au 24 Janvier 2014 ==		== Semaines de modules transversaux : du 6 au 10 Janvier 2014, du 13 au 17 Janvier 2014, du 20 au 24 Janvier 2014 ==
−	Programmations d'une interface graphique sur Matlab fichier GUI Graphical User Interfaces	+	Programmation d'une interface graphique sur Matlab appelé GUI (Graphical User Interfaces) avec un fichier nommé '''Interface_Essai.fig''' :
		+
		+	[[Fichier: Interface_Essai.fig.JPG|1000px|thumb|center|'''Photo de la programmation de l'interface graphique GUI''']]
		+
		+	Export au format script nommé '''Interface_Essai.m'''
		+
		+	Ajout de code pour traitement
		+
		+	global g_x1;
		+
		+	Cette instruction déclare la variable g_x1 en globale
		+
		+	g_x1 = str2num(get(handles.x1,'string'));
		+
		+	Cette instruction définit g_x1 égale la valeur de l'edit text x1
		+
		+	L'instruction ''handles'' sert à définir l'utilisation d'un Tag
		+
		+	L'instruction ''get'' retourne la valeur de propriété spécifique de l'objet graphique avec des poignées
		+
		+	L'instruction ''str2num'' convertie un char (string) en nombre (double)
		+
		+	assignin('base','x1',g_x1);
		+
		+	Cette instruction définit la variable ''x1'' dans le Workspace et lui attribut la valeur de g_x1
		+
		+	Les mêmes instructions sont définit pour g_x2, g_x3, g_y1, g_y2, g_y3, g_z1, g_z2 et g_z3
	== Semaine du 28 au 31 Janvier 2014 ==		== Semaine du 28 au 31 Janvier 2014 ==
		+	Création d'un programme '''Northstar_startup.m''' qui redéfinit le chemin pour atteindre les répertoires ''blockset'' et ''toolbox''
		+
		+	addpath('C:\Documents\Cours Polytech\Semestre 9\PFE\Didactic\RobotinoMatlab\blockset');
		+	addpath('C:\Documents\Cours Polytech\Semestre 9\PFE\Didactic\RobotinoMatlab\toolbox');
		+
		+	Création d'un programme '''Northstar_param_dichotomie.m'''
		+
		+	fonction principale :
		+
		+	a = calib_min;
		+	b = calib_max;
		+
		+	c = (a+b)/2;
		+	iter=0
		+
		+	while norm(func(c))>=epsi && iter<nb_it_max
		+
		+	if x_N_c == x_O_c && y_N_c == y_O_c && z_N_c == z_O_c
		+	calib_final = c;
		+	end
		+
		+	if abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) && abs(y_N_c-x_N_a) < abs(y_N_c-x_N_b) || ...
		+	abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) && abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) || ...
		+	abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) && abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b)
		+
		+	b=c;
		+	c=(a+c)/2;
		+	else
		+	a=c;
		+	c=(b+c)/2;
		+	end
		+
		+	iter=iter+1;
		+
		+	end
		+
		+	calib_final = c;
		+
		+	== Semaine du 4 au 7 Février 2014 ==
		+
		+	''' Erreurs de compilation fichier init.m '''
		+
		+	Warning: Name is nonexistent or not a directory: \bin\x64.
		+	> In path at 110
		+	In init at 20
		+	Warning: Name is nonexistent or not a directory: \include\rec\robotino\com\c.
		+	> In path at 110
		+	In init at 21
		+	??? Error using ==> loadlibrary>lFullPath at 613
		+	Could not find file Com.h.
		+
		+	Error in ==> loadlibrary at 226
		+	header=lFullPath(header);
		+
		+	Error in ==> init at 22
		+	loadlibrary( 'rec_robotino_com_c.dll', 'Com.h', …
		+
		+
		+	''' Correction du fichier init.m '''
		+
		+	code initial :
		+
		+	robotinoMatlabDir = getenv('ROBOTINOMATLAB_DIR');
		+	robotinoMatlabINC1 = strcat( robotinoMatlabDir, '\include\rec\robotino\com\c' );
		+	robotinoMatlabINC2 = strcat( robotinoMatlabDir, '\include' );
		+
		+	modification :
		+
		+	robotinoMatlabDir = 'C:\Program files\Didactic\RobotinoMatlab';
		+	robotinoMatlabINC1 = 'C:\Program files\Didactic\RobotinoMatlab\include\rec\robotino\com\c';
		+	robotinoMatlabINC2 = 'C:\Program files\Didactic\RobotinoMatlab\include';
		+
		+	''' Toujours 2 messages d'erreurs '''
		+
		+	Error using ==> loadlibrary at 282
		+	Microsoft Visual C++ 2005 or 2008 is required to use this feature.
		+
		+	Error in ==> init at 20
		+	loadlibrary( 'rec_robotino_com_c.dll', 'Com.h')
		+
		+	''' Utilisation de l'instruction : >> mex -setup , qui permet de définir le compilateur '''
		+
		+	Les fonctions Matlab écrits en C + + sont appelés MEX-files. MEX signifie Matlab EXectuable. Les MEX-files sont liés de façon dynamique sous-programmes produits à partir de
		+	C / C + + ou Fortran. Ces fichiers contiennent des extension ''.dll''. La principale raison d'écrire un MEX-file est d'utiliser C pré-existant / C++ ou Fortran routines Matlab
		+	sans avoir à les recoder.
		+
		+	Welcome to mex -setup.  This utility will help you set up
		+	a default compiler.  For a list of supported compilers, see
		+	http://www.mathworks.com/support/compilers/R2011a/win64.html
		+
		+	Please choose your compiler for building MEX-files:
		+
		+	Would you like mex to locate installed compilers [y]/n? y
		+
		+	Select a compiler:
		+	[1] Microsoft Visual C++ 2005 SP1
		+	[2] Microsoft Visual C++ 2010
		+
		+	[0] None
		+
		+	Compiler: 0
		+
		+	mex: No compiler selected. No action taken.
		+
		+	Warning: The MATLAB C and Fortran API has changed to support MATLAB
		+	variables with more than 2^32-1 elements.  In the near future
		+	you will be required to update your code to utilize the new
		+	API. You can find more information about this at:
		+	http://www.mathworks.com/support/solutions/en/data/1-5C27B9/?solution=1-5C27B9
		+	Building with the -largeArrayDims option enables the new API.
		+
		+	''' Solutions envisagées : '''
		+
		+	Désinstallation puis réinstallation dans cette ordre avec teste entre chaque de :
		+
		+	- Microsoft Visual Studio 8
		+
		+	- Microsoft Visual Studio 9
		+
		+	- Microsoft Visual Studio 10
		+
		+	- Microsoft Visual C++ 2005
−	== Semaine du 4 au 7 Février 2014 ==	+	- Microsoft Visual C++ 2008
		+	- Microsoft Visual C++ 2010
		+
		+	Puis en parlant avec un doctorant travaillant aussi sur Matlab, qui m'a dit que le problème venait du PC sur lequel était compilé les programmes.
		+
		+	Car c'est un PC 64 bits et que Matlab ne fonctionne pas de la même façon sur un PC 32 bits et 64 bits.
		+
		+	En cherchant ensemble sur internet, apparemment ça serait un problème de librairie mais sans savoir laquelle il m'a proposé la solution qu'il a utilisé lors d'une démonstration pour l'université : c'est de faire une partition du PC avec :
		+
		+	- une partition de Windows 7 en 64 bits
		+
		+	- une partition de Windows 7 en 32 bits
		+
		+	Mais avant de faire ça sur un PC, j'ai vérifié et il y a 2 PCs 64 bits et 2 PCs 32 bits.
		+
		+	Donc à partir de ce moment, la compilation se fait sur Matlab sur un PC 32 bit.
	== Semaine du 10 au 14 Février 2014 ==		== Semaine du 10 au 14 Février 2014 ==
		+	Modifications du programme Northstar.m pour imbriquer les conditions d'utilisation des valeurs obtenues par le capteur Nothstar et voir d'où venait les erreurs si c'était le cas
		+
		+	4 conditions :
		+
		+	(1) S’il n’y a aucune détection du capteur
		+	C’est-à-dire s’il ne capte aucun spot lumineux et que leurs intensités sont nuls
		+
		+	if ( NorthStar_magSpot0(NorthStarId) ~= 0 && NorthStar_magSpot1(NorthStarId) ~= 0 ...
		+	&& NorthStar_numSpotsVisible(NorthStarId) ~= 0)
		+
		+	(2) Si la détection est trop faible
		+	C’est-à-dire si le capteur capte les 2 spots lumineux et que chacun d’eux  une intensité supérieur à un pourcentage, ici 3 %
		+
		+	if (NorthStar_magSpot0(NorthStarId)/1000 > 3 && NorthStar_magSpot1(NorthStarId)/1000 > 3 ...
		+	&& NorthStar_numSpotsVisible(NorthStarId) == 2)
		+
		+	(3) Si les valeurs du capteur Northstar semblent incohérentes
		+	C’est-à-dire si pour une vitesse non nulle selon x, y ou phi, la valeur de la position ne doit pas être égale à 0
		+
		+	if (Vx~=0 || Vy~=0 || Vphi~=0) && ...
		+	(Nx~=0 && Ny~=0 && Nphi~=0)
		+
		+	(4) Si l’écart entre les valeurs de l’Odométrie et celles de Northstar sont assez importantes
		+	C’est-à-dire si l’erreur entre la valeur du capteur Northstar et celle par Odométrie pour chaque variable x, y et phi est supérieur à la variable erreur_O_N qui est la valeur d‘erreur acceptable vis-à-vis de la précision du capteur Northstar
		+
		+	if (abs(Ox - Nx) > erreur_O_N && abs(Oy - Ny) > erreur_O_N ...
		+	|| abs(Ox - Nx) > erreur_O_N && abs(Ophi - Nphi) > erreur_O_N ...
		+	|| abs(Oy - Ny) > erreur_O_N && abs(Ophi - Nphi) > erreur_O_N)
		+
		+	Si ces 4 conditions sont remplies les valeurs utilisées sont celles du capteur Northstar
		+
		+	x = Nx;
		+	y = Ny;
		+	phi = Nphi;
		+
		+	Sinon ceux sont celles obtenues par le capteur par Odométrie
		+
		+	x = Ox;
		+	y = Oy;
		+	phi = Ophi;
		+
		+	La condition la plus gênante était d'avoir des valeurs aberrantes : le problème était d'abord de savoir sous quelles conditions, on peut les considérer aberrantes et quelle peut être l'origine.
	== Semaine du 17 au 21 Février 2014 ==		== Semaine du 17 au 21 Février 2014 ==
		+	'''Programme par dichotomie'''
		+
		+	4 conditions :
		+
		+	(1) Si la valeur par Odométrie de x, y et phi est dans l’intervalle [a, c] des valeurs de Northstar
		+
		+	if (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc) && (phiNa <= phiO && phiO <= phiNc)
		+
		+	(2) Si la valeur par Odométrie de x, y et phi est dans l’intervalle [c, b] des valeurs de Northstar
		+
		+	elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb) && (phiNc <= phiO && phiO <= phiNb)
		+
		+	(3) Si la valeur par Odométrie de x et y (en négligeant une erreur sur phi) est dans l’intervalle [a, c] des valeurs de Northstar
		+
		+	elseif (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc)
		+
		+	(4) Si la valeur par Odométrie de x et y (en négligeant une erreur sur phi) est dans l’intervalle [c, b] des valeurs de Northstar
		+
		+	elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb)
		+
		+	Si les valeurs sont dans l'intervalle de calibration [a, c]
		+
		+	b=c;
		+	c=(a+c)/2;
		+
		+	Si les valeurs sont dans l'intervalle de calibration [c, b]
		+
		+	a=c;
		+	c=(b+c)/2;
		+
		+	Première Modification :
		+
		+	Changement de un seul epsilon ''epsi'' mais dans un second temps, il en utilisait deux, un pour les valeurs en millimètre (x et y) : ''epsi_mm'' et un pour les valeurs en degrés (phi) : ''epsi_deg''.
		+
		+	Avant modification :
		+
		+	(abs(xNc - xO)>=epsi || abs(yNc - yO)>=epsi || abs(phiNc - phiO)>=epsi)
		+
		+	Après :
		+
		+	(abs(xNc - xO)>=epsi_mm || abs(yNc - yO)>=epsi_mm || abs(phiNc - phiO)>=epsi_deg)
		+
		+	Seconde Modification :
		+
		+	Au lieu de regardé si les valeurs sont dans l'intervalles de calibration [a, c] ou [c, b], le programme cherche si les valeurs sont inférieur ou supérieur avec la calibration de c :
		+
		+	Avant modification :
		+
		+	if (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc) && (phiNa <= phiO && phiO <= phiNc)
		+	elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb) && (phiNc <= phiO && phiO <= phiNb)
		+	elseif (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc)
		+	elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb)
		+
		+	Après :
		+
		+	if xO <= xNc && yO <= yNc && phiO <= phiNc)
		+	elseif xNc <= xO && yNc <= yO && phiNc <= phiO
		+	elseif xO <= xNc && yO <= yNc)
		+	elseif xNc <= xO && yNc <= yO
		+
		+	'''Programme pas à pas'''
		+
		+	Le programme de dichotomie ayant toujours des défauts de recherches
		+
		+	Création d'un autre programme pas à pas, même principe que la dichotomie, mais il balaye tout l'intervalle de calibration.
		+
		+	D’abord pour trouver les extrêmes de l'intervalle de départ de recherche du programme par dichotomie, c'est-à-dire les valeurs (x, y et phi) du capteur Northstar sont différentes de 0.
		+
		+	Puis pour trouver l'intervalle dans lequel devrait se trouver le résultat de la recherche par dichotomie, c'est-à-dire si la différence entre les valeurs (x, y et phi) du capteur Northstar et celles de l’Odométrie sont inférieurs aux valeurs epsi_mm et epsi_deg, utilisées dans l’algorithme de dichotomie.
		+
		+	== 24 Février 2014 ==
		+
		+	Mise à jour des Gantt
		+
		+	Travail sur le rapport et le Wiki
	== 25 Février 2014 ==		== 25 Février 2014 ==
−	Rendu du Rapport final de projets	+	Rendu du Rapport final de projet
		+	== 26 Février 2014 ==
		+
		+	Travail PowerPoint pour la soutenance
	== 27 Février 2014 ==		== 27 Février 2014 ==
	Soutenances finales de projets		Soutenances finales de projets
		+
		+	= Résultats =
		+
		+	== Sur RobotinoView ==
		+
		+	Parcours d’un rectangle de 1 m sur 50 cm :
		+
		+	[[Fichier: Courbes_RobotinoView_a_echelle.JPG|650px|thumb|left|'''Courbes RobotinoView avec valeurs de Northstar point pas point''']]
		+
		+	[[Fichier: Courbes_RobotinoView_relié_a_echelle.JPG|650px|thumb|right|'''Courbes RobotinoView avec valeurs de Northstar en continu''']]
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+	Ces graphiques montrent que l'on a un écart maximum de 10 cm or dans la documentation, il est dit que le capteur Northstar a une précision de +/- 5 cm; ce qui correspond
		+
		+	== Sur Matlab ==
		+
		+	Pour le même parcours
		+
		+	[[Fichier: Courbes_Matlab_avec_Northstar.JPG|800px|thumb|left|'''Courbes Matlab''']]
		+
		+	[[Fichier: Courbes_Matlab_avec_Northstar_zoom_l'échelle.JPG|540px|thumb|rightt|'''Courbes Matlab avec zoom sur les consignes''']]
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+
		+	Sur le graphique de gauche on voit que les valeurs de Northstar sont de 2 à plus 100 fois plus grandes c'est-à-dire jusqu’à quelques mètres d'erreurs.
		+
		+	Alors que sur le graphique de droite, on voit un zoom sur les valeurs de consigne qui permet de voir que les valeurs par Odométrie sont aussi précises.
		+
		+	= Gestion de projet =
		+
		+	== Planning prévisionnel ==
		+
		+	Planning prévisionnel sous forme de Gantt fixé au début du projet et refixé à partir de la soutenance intermédiaire :
		+
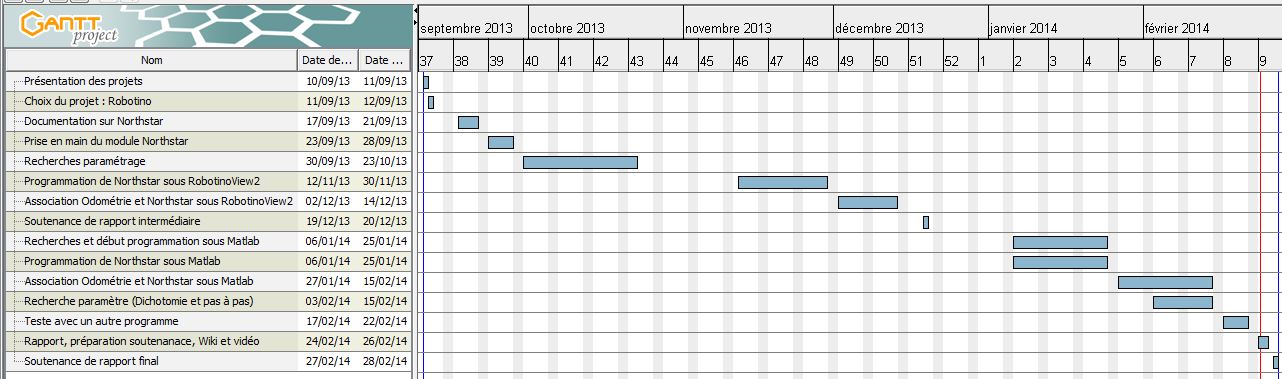
		+	[[Fichier: PFE_Gantt_prévisionnel.JPG|1000px|thumb|center|'''Gantt prévisionnel''']]
		+
		+	Ce Gantt fait au début des deux parties du projet devait me servir de fil conducteur pour estimer ma progression et mon retard si cela était le cas.
		+
		+	== Planning réel ==
		+
		+	Planning réel sous forme de Gantt pour voir à quoi est dû l'écart entre le planning prévisionnel et réel :
		+
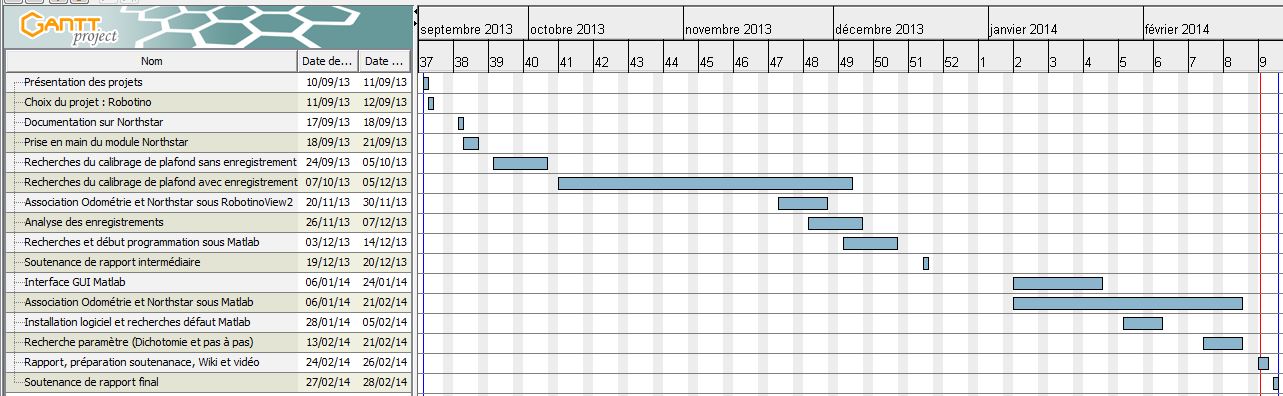
		+	[[Fichier: PFE_Gantt_réel.JPG|1000px|thumb|center|'''Gantt réel''']]
		+
		+	Les points non suivis :
		+
		+	- Durée des temps de recherches plus court
		+
		+	- Durée des temps de prise en mains plus court
		+
		+	Les points non ou mal évalués :
		+
		+	- Temps de programmation sur RobotinoView et Matlab (trop court car déjà utilisé mais points complètement nouveaux)
		+
		+	- Temps perdu lié à la compatibilité des logiciels ou des librairies et mise à jour
		+
		+	Les points ajoutés :
		+
		+	- Programmation de l’analyse avec Matlab des résultats
		+
		+	- Teste d'autres modes de recherche de paramétrage (en premier abord la dichotomie devait suffire)
		+
		+	- Programmation interface graphique GUI Matlab
		+
		+	= Rapport =
		+
		+	[[Fichier: Rapport_PFE_Lenormand_Mathieu.pdf‎]]
	= Annexes =		= Annexes =
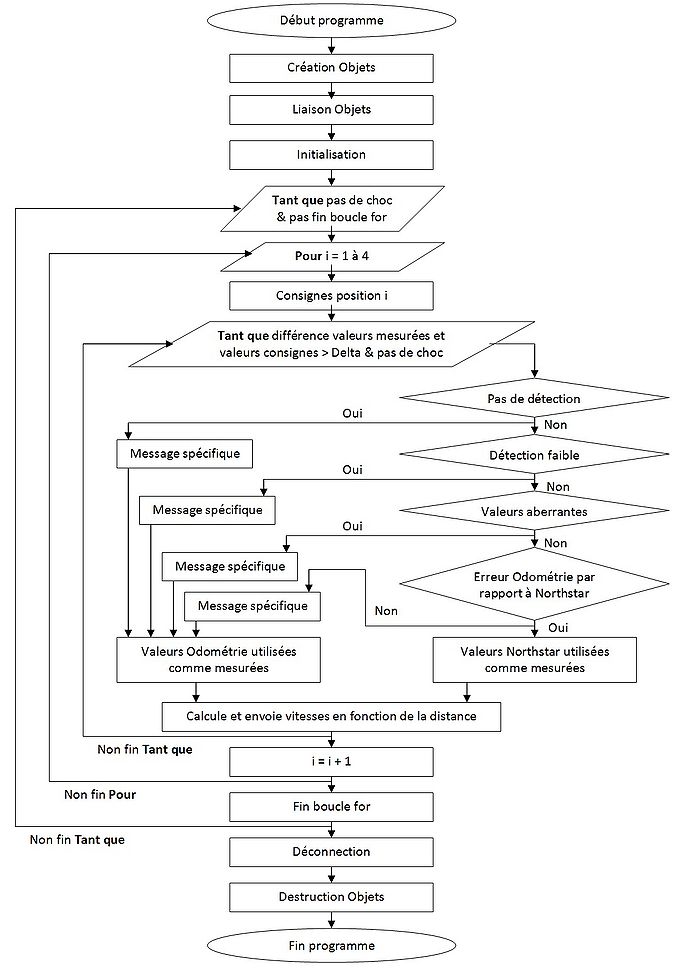
−	== Fichier Matlab Analyse_Sorties.m ==	+	== Ordinogramme du programme Northstar sur Matlab ==
−	== Fichier Matlab Northstar.m ==	+	[[Fichier: Ordinogramme_du_programme_Northstar.jpg|700px|thumb|center|'''Ordinogramme du programme Northstar sur Matlab''']]

---

Version actuelle datée du 26 juin 2014 à 16:03

Présentation du Robotino

Le Robotino est un robot mobile, avec un châssis rond en inox et trois unités de motorisation omnidirectionnelles

Ses dimensions sont :

- Diamètre : 370 mm

- Hauteur (habillage compris) : 210 mm

- Poids total : environ 11 kg

Les informations de commandes sont envoyées par Wifi via un routeur dédié présent dans la salle Robotino.

Pour la programmation, il existe le logiciel RobotinoView2 qui est un logiciel de programmation du Robotino conçu par Festo. Le Robotino peut être programmé avec d'autres logiciels, Matlab principalement car à l'installation, il y a une toolbox Matlab associé aux blocs fonction du logiciel avec RobotinoView2 ou en utilisant d'autres langages de programmation comme le C++ et Java.

Les capteurs présents initialement sur le Robotino sont :

- 1 Structure de protection en caoutchouc intégrant un détecteur anticollision

- 9 capteurs de distance analogiques à infrarouge

- 1 capteur inductif analogique

- 2 capteurs optiques numériques

Auxquels, on ajoute généralement 1 caméra Web couleur à interface USB.

Avec cette bases de capteurs beaucoup de TPs sont réalisés à Polytech.

Mais pour des projets ou des applications particulières, Festo vend des modules supplémentaires pour le Robotino, tel que le module Northstar de ce projet.

Présentation du projet

Contexte

Pour mon projet de l’année dernière, j’ai utilisé les fonctions de traitement d’image de RobotinoView2, le logiciel de Festo pour programmer le Robotino. La même année, j’ai utilisé lors des Travaux Pratiques de Robotique, la fonction d’odométrie du Robotino. L’odométrie est une technique permettant d'estimer la position d'un véhicule en mouvement. Le terme vient du grec hodos (voyage) et metron (mesure). Cette mesure est présente sur quasiment tous les robots mobiles, grâce à des capteurs embarqués permettant de mesurer le déplacement du robot (de ses roues). Le principe de l’odométrie repose sur la mesure individuelle des déplacements des roues, en comptant les incrémentations du moteur, pour reconstituer le mouvement global du robot. En partant d'une position initiale connue et en intégrant les déplacements mesurés, on peut ainsi calculer à chaque instant la position courante d’un robot mobile.

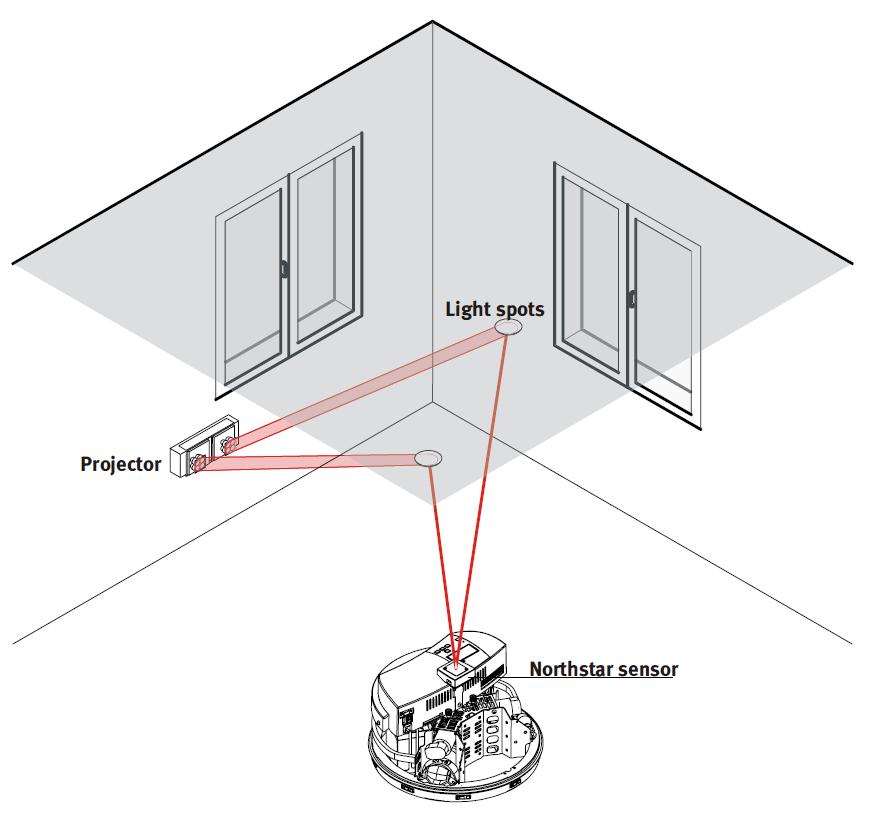
C’est pourquoi cette année, j’ai eu l’opportunité d’utiliser le module Northstar qui est un système de localisation indoor acquis par Polytech’Lille, comparable à un système de géo-localisation dans un plan. Ce système de navigation associe un projecteur et un capteur infrarouge.

Remarque : il existe 2 types de projecteur, type NS1 et NS2, sur ce schéma c'est un type NS1. Et lors de ce projet, c'est un projecteur de type NS2 qui était fournit. La différence principale est sur la plage de fréquences dans laquelle émet le projecteur sinon le fonctionnement est le même.

Cahier des charges

Objectif principal :

Tester l’association de capteurs sur une trajectoire quelconque.

Appliquer cela à des cas concrets, d’abord des trajectoires assez simples, sur des problèmes tels que le patinage ou le glissement des roues qui créent des erreurs avec l’odométrie. Puis en associant mes résultats au projet d’un doctorant qui travail sur l’évitement d’obstacle avec le Robotino par la logique floue.

Objectifs liés au module Northstar :

- Comprendre le fonctionnement du module Northstar.

- Savoir paramétrer et initialiser le projecteur et le capteur.

- Prendre en mains le bloc associé à Northstar sur RobotinoView2.

- Etudier la précision du module Northstar (selon les consignes, la vitesse, la lumière...)

- Rendre le positionnement dans l’espace le plus précis possible, après ces étapes, c’était l’objectif en associant les valeurs de x, y et phi calculées par l’odométrie et par le module Northstar le plus précis possible.

Contraintes :

- Le terrain

- La sensibilité des capteurs

- La vitesse

- La fiabilité

Moyens d’actions :

Les capteurs déjà utilisés :

- Un odomètre

- Un gyroscope

Un nouveau capteur :

- Un module Northstar

Journal de bord

10 Septembre 2013

Présentation des projets IMA 5

11 Septembre 2013

Rencontre avec les professeurs pour avoir plus de détails sur les projets, suivi du choix et de l'attribution des projets

17 Septembre 2013

Discutions avec Mr Rochdi MERZOUKI sur le projet en lui même et ses objectifs.

Prise de contact avec Mr Olivier SCRIVE pour récupérer la boîte contenant le module Northstar

Ecriture d'un diagramme de Gantt pour la gestion du projet, avec les premières étapes du projet ainsi qu'une estimation de leur durée

18 Septembre 2013

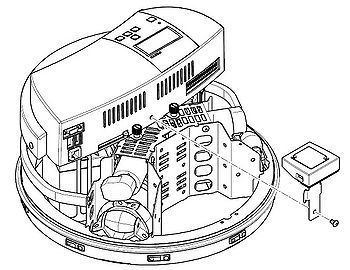
Découverte du kit Northstar qui comprend :

- 1 capteur Northstar

- 1 câble USB pour le relier le capteur au Robotino

- 1 projecteur avec un trépied

- 1 bloc d’alimentation électrique adaptable aux prises internationales

- 1 câble pour relier le projecteur au bloc d’alimentation

- 1 manuel d’utilisation (allemand et anglais)

Assemblage du projecteur avec le trépied et le bloc alimentation ainsi que du capteur Northstar avec le Robotino.

Prise en main du bloc Northstar présent sur le logiciel RobotinoView2

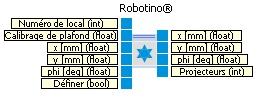
Les entrées sont :

- Numéro de local correspondant au numéro du local dans lequel Robotino se trouve, lié au numéro fixé sur le projecteur

- Calibrage du plafond (en mm) correspondant à la distance entre le détecteur et le plafond

- X (en mm) correspondant à la position x de l'origine définie par l'entrée "Définir"

- Y (en mm) correspondant à la position y de l'origine définie par l'entrée "Définir"

- Phi (en mm) correspondant à la position phi de l'origine définie par l'entrée "Définir"

- Définir correspondant à un booléen, si vrai (true) la pose (x,y,phi) est prise pour origine

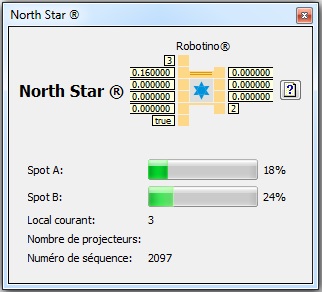
Prise de l'interface du bloc Northstar quand le programme est lancé

Sur cette interface, on peut lire :

- le pourcentage de détection des 2 spots : Spot A et Spot B

- le numéro du local courant

- le nombre de projecteurs détecté par le capteur

- le numéro de séquence qui correspond au nombre de fois où le capteur à tenter de capter les spots depuis le lancement du programme.

24 Septembre 2013

Ecriture d'un sous programme nommé Northstar sous RobotinoView2 qui commande le Robotino avec un bloc appelé panneau de commande et qui calcule en même temps la différence entre les valeurs avec le capteur Northsatr et celles par odométrie

Pour les premiers programmes, le choix était d'envoyer la lumière du projecteur se réfléchir sous un bureau dans l'idée d'avoir un plafond plus bas et donc un meilleur pourcentage de captation.

Ce qui est le cas car pour un périmètre de 0 à 1,5 m, on obtient pour les spot A et spot B des valeurs entre 85 et 98 %.

Avec un paramétrage :

calibrage du plafond : 500 pour avoir des valeurs acceptables sachant que normalement le bureau fait 1,2 m donc cette valeur

numéro du local : 5

calibrage du projecteur : 3

C'est 2 valeur sont liés car si on associe pas les bonnes valeurs, on ne capte pas le signal. Mais à ce stade ce couple pris sur un exemple suffisait, l'explication sera faite par la suite.

25 Septembre 2013

Ecriture d'un sous programme nommé Odometrie_auto qui utilise le bloc Odométrie :

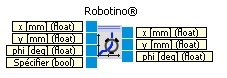
pour commander le déplacement du Robotino d'une position d'origine à une autre position, en définissant une position comme un vecteur de à 3 composantes x, y et phi.

Les entrées x, y et phi sont les valeurs de la positions à atteindre.

L'entrée Spécifier sert à démarrer le fonctionnement du bloc.

Et les sorties sont les valeurs courantes de x, y et phi.

30 Septembre 2013

Ecriture d'un sous programme nommé Drive qui prend utilise les valeurs de Northstar plus un delta égale à la différence entre les valeurs par odométrie et celles avec le capteur Northsatr, pour commander le déplacement du Robotino d'une position d'origine à une position d'arrivée.

A ce stade, il y a 2 blocs constante nommé boolean et position à modifier pour lancer le programme associé à 3 étapes :

Etape 1 : définition origine :

boolean = 1

position = 1

Etape 2 : lancement odométrie et northstar :

boolean = 0

position = 1

Remarque sur l'étape : légères oscillations autour de la position d'origine dû à la précision de Northstar

Etape 3 : commande d'avancement d'une valeur entre 0 et 2 m selon X :

boolean = 0

position = 2

Remarques sur l'étape : même oscillations autour de la position d'arriver avant de la considérer comme atteinte.

1 Octobre 2013

Ecriture d'un sous programme nommé Moyenneur sous RobotinoView2 qui fait la moyenne entre les valeurs de x, y et phi obtenues par odométrie et par le capteur Northstar.

Ce programme s'inspire du programme Drive en changeant la formule pour le calcul de la position.

2 Octobre 2013

Les résultats obtentions par ces programmes paraissaient aberrants par des mesures avec un mètre à ruban et des marquages avec du scotch blanc au sol.

Recherches d'informations sur le paramétrage.

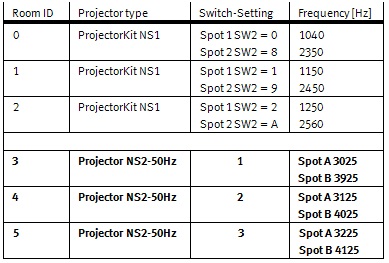
D'abord le premier point était de comprendre le lien entre le numéro du local qui est définie sur le bloc Northstar sur RobotinoView2 et le calibrage du projecteur qui est définit directement sur le projecteur par une molette. (point laissé en suspend le 24 Septembre)

Il y a 3 configurations possibles du au fait de l'utilisation d'un projecteur de type NS2 :

- Calibrage du projecteur (switch-setting) = 1 et numéro du local (Room ID sur le bloc Northstar) = 3

- Calibrage du projecteur (switch-setting) = 2 et numéro du local (Room ID sur le bloc Northstar) = 4

- Calibrage du projecteur (switch-setting) = 3 et numéro du local (Room ID sur le bloc Northstar) = 5

Ces combinaisons servent à définir différents locales ou espaces de travail dans le cas où on a différents projecteurs par exemple. Car pour chaque configuration le projecteur et le capteur travaille à des valeurs de fréquences différentes.

7 Octobre 2013

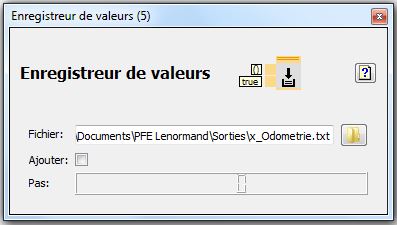
Modification du programme Odometrie_auto renommé Odometrie_consig_Northstar_enregistr pour qu'il continue à commander la Robotino avec les valeurs d'odométrie et qu'il enregistre aussi les valeurs grâce au bloc nommé Enregistreur de valeurs qui inscrit les valeurs d'entrée, séparées par un tabulateur, sur une nouvelle ligne du fichier texte.

Ces fichiers texte sont contenus dans un dossier nommé Résultats, il y en a 6 fichiers texte :

- x_Northsyar

- y_Northstar

- phi_Northstar

- x_Odometrie

- y_Odometrie

- phi_Odometrie

Le nom et le chemin de stockage de chaque fichier texte est à définir dans l'interface du bloc Enregistreur de valeurs.

Grâce à ces fichiers texte, à l'affichage des valeurs de connexions et par une méthode empirique, la valeur de calibrage du plafond a été définit.

14 Octobre 2013

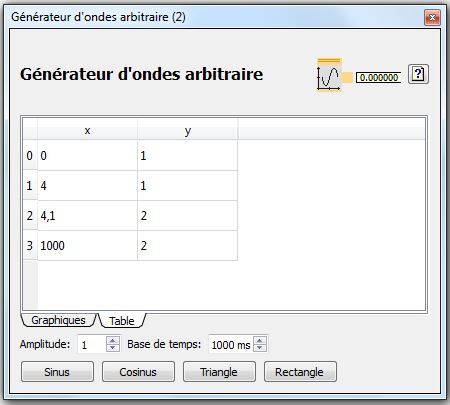
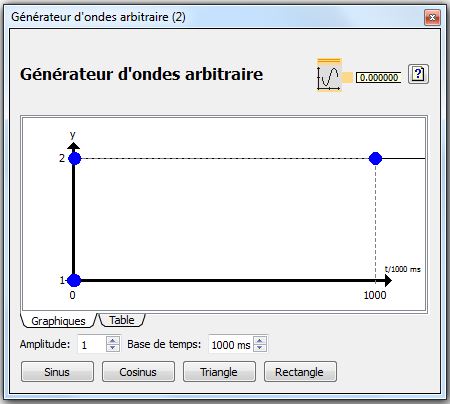
Modifications des programmes, utilisation de blocs Générateur d'ondes arbitraire :

qui sert à faire le changement de positions en commandant dans le temps les variables du programme boolean et position avec les étapes

Etape 1 : définition origine :

boolean = 1 et position = 1

Etape 2 : lancement odométrie et northstar :

boolean = 0 et position = 1

Etape 3 : commande d'avancement sur la position 2 :

boolean = 0 position = 2

C'est en modifiant dans l'interface de ces bloc soit de façon graphique soit dans un tableau que cela permettait de définir les valeurs des variables boolean et position qui serviraient à définir ces 3 étapes au cours du temps

Remarque pour une meilleur précision, le programme effectue ces 3 étapes entre 2 positions pour redéfinir la position de départ à chaque fois et avoir un meilleur résultat.

15 Octobre 2013

Ecriture de 3 sous programme nommé Northstar_x, Northstar_y et Northstar_phi avec 1 position selon les axes :

- Northstar_x : 1ère position (1000, 0, 0) : déplacement de 1 m selon l'axe X

- Northstar_y : 2ème position (0, 500, 0) : déplacement de 0,5 m selon l'axe X

- Northstar_phi : 3ème position (0, 0, 180) : déplacement de 180° sur lui même

Ce teste donne des résultats assez concluant selon l'axe X et l'axe Y. Mais des erreurs selon Phi, cela a été supposé lié à la précision de Northstar.

Cependant cela était dû à la variable booléenne utilisée pour définir la position atteinte. Les erreurs selon Phi ont été laissé de côté, jusqu'au 28 Novembre, date à laquelle l'origine a été découverte en faisant des enregistrements de trajectoires.

16 Octobre 2013

Ecriture d'un sous programme nommé Northstar_pgr qui sera un sous programme générique car dans la version précédente, il y avait un sous programme par position (Northstar_x, Northstar_y et Northstar_phi) ce qui était redondant et lourd.

Ecriture d'un nouveau sous programme nommé Northstar_pgr_avec_inc qui correspond au programme Northstar_pgr avec l'incrémentation de la position dans ce sous programme.

22 Octobre 2013

Rédaction du rapport et modifications sur le Wiki car tous les Robotinos étaient occupés par une séance de TP.

23 Octobre 2013

Jusqu'à présent les testes et le travaille effectué se faisant sur le Robotino numéro 16 avec comme adresse IP 172.26.94.16. Mais à cette séance, ce Robotino était utilisé par une autre classe, c'est pourquoi cette séance et les suivantes se sont faites avec le Robotino numéro 17 avec comme adresse IP 172.26.94.17.

Cependant avec ce changement de Robotino, les valeurs obtenues qui ne correspondaient pas. C'est pourquoi, de façon empirique, une nouvelle valeur de calibrage du plafond égale à 3900 a été obtenu, alors que la valeur théorique devrait être 2600 (2,8 m de hauteur de plafond moins 0.2 m de hauteur du Robotino).Donc la valeur est au dessus et que pour le numéro 16, la valeur était en dessous.

De plus avec cette nouvelle de calibrage avec la table comme plafond une autre recherche est faite pour le calibrage du plafond de la salle et donc l'utilisation pour la suite du Robotino sur la piste.

Le projecteur est posé sur une chaise pour 2 raisons :

- pour éviter un choque direct avec le Robotino si il y a une erreur de programmation de la trajectoire

- pour avoir une meilleur distinction des spots car plus en hauteur donc plus près du plafond

13 Novembre 2013

Problème d'incrémentation avec sous programme nommé Northstar_pgr_avec_inc car il incrémente trop vite et donc ne passe pas par toutes les positions.

Ecriture d'un sous programme nommé Incrementer_pos qui ne s'occupe que de l'incrémentation de la position et associé au sous programme Northstar_pgr dans le programme principale, cela permet de parcourir plusieurs positions.

Problèmes : ne fait que 3 positions sur les 5 demandées dans le teste du programme, modifications en cours.

20 Novembre 2013

Ecriture d'un sous programme nommé Northstar_sup_odo qui utilise un bloc Multiplexeur pour d'abord prendre pour consigne l'odométrie et la remplacer par Northstar quand erreur supérieur à une valeur départ de " 100 mm " car d'après le guide, on sait que Nothstar a une précision de +/- 50 mm

Bon fonctionnement du programme sur 2 m selon X

26 Novembre 2013

Rencontre avec 2 doctorants dont Achille qui travaille sur l’évitement d’obstacle avec le Robotiono par la logique floue.

Proposition leur part de faire des graphique et des courbes des valeurs enregistrées dans des fichiers texte et qui étaient d'habitude utilisées surtout pour le paramétrage. Et d'analyser ces courbes pour voir l'influence des trajectoires, de la vitesse et de la lumière sur la précision entre l'Odométrie et Northstar.

Ensuite, ils m'ont proposé changer le programme écrit sous RobotinoView2 au format Matlab grâce à une toolbox dédié, pour pouvoir intéragir avec le programme basé sur la logique floue d'Achille en lui donnant la meilleur précision de localisation.

Teste de la lumière, il n'y a aucune influence à 17h fin novembre lumière éteinte ou allumée. Ce qui était envisageable car le projecteur et le capteur travaillent dans le domaine de l'infrarouge.

Ecriture d'un programme Matlab nommé Analyse_Sorties.m qui quand il est exécuté dans un dossier contenant les 6 fichiers textes (x, y et phi selon l'odométrie et Northstar) récupère directement ces valeurs grâce à la fonction textread et les place dans des vecteurs du même nom.

Et avec la fonction plot, les courbes sont représentés sur des graphiques.

27 Novembre 2013

Modifications du programme Matlab nommé Analyse_Sorties.m, d'abord en rajoutant un titre et des légendes aux graphiques.

Ensuite le problème de représentation est lié que le capteur odométrie fonctionne a une fréquence plus élevé, environ 3 fois plus rapide que le capteur Northstar, c'est-à-dire que pour une valeur mesurée avec le capteur Northstar, le capteur d'odométrie en aura mesuré 3. Mais cela varie encore selon la vitesse du Robotino et que se soit la variable x, y ou phi que l'on mesure.

C'est pourquoi, pour avoir une représentation à l'échelle sans mesurer le temps en plus, les valeurs mesurées par odométrie sont représenté sur les graphiques par un pas égale à 1 et celles mesurées avec Nothstar par un pas égale à la division du nombre de valeurs enregistrées par odométrie par le nombre de valeurs enregistrées par Northstar.

Exemple avec une consigne de 2000 mm selon x :

De plus ce fichier calcul le plus grand écart type. Cependant pour ce calcul, le problème s'est posé dans l'autre sens, car la fonction std qui calcul l'écart type ne s'applique que sur des vecteurs de même taille. Il a fallu retiré des valeurs aux vecteurs contenant les valeurs enregistrées par odométrie, car ceux sont eux les plus grands dû à la vitesse d'enregistrement. Et qu'il est plus logique de retirer des valeurs que d'en inventer.

A partir de ce moment, les enregistrements ont été refait, le dossier de stockage des enregistrements de x, y et phi par odométrie et Northstar n'est plus nommé Résultats mais Sorties. Et le dossier Résultats contient maintenant des dossiers dont le nom évoque la trajectoire effectuée par le Robotino avec comme consigne les valeurs d'odométrie et comme enregistrements celles par odométrie et par Nothstar.

Les dossiers correspondant aux trajectoires sont :

- Selon X (2m)

- Selon Y (1m)

- Trajectoire diagonale (Combinaison X (1m) et Y (1m))

28 Novembre 2013

Nouveaux dossiers correspondant à de nouvelles trajectoires :

- Selon Phi (tour sur lui même)

- Trajectoire circulaire (Combinaison X (1m) et Phi (180°))

- Trajectoire circulaire (Combinaison Y (1m) et Phi (180°))

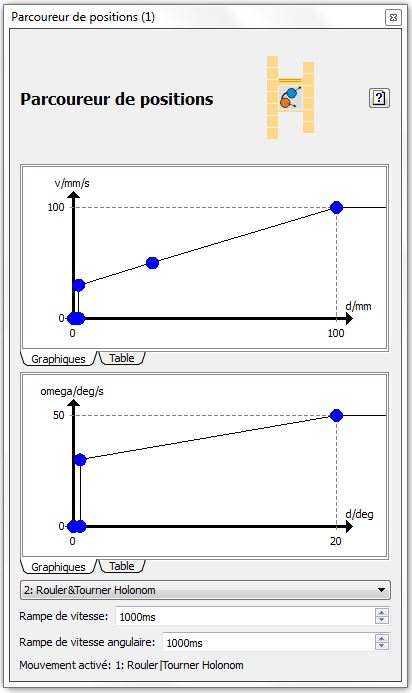
Cependant les trajectoire avec phi ne répondait pas selon cette variables alors après vérification du programme RobotinoView2 dans lequel, un bloc nommé Parcoureur de positions est utilisé.

C'est ce bloc qui calcule la vitesse x, y et angulaire en fonction de la position (x, y et phi) de consigne et de la position (x, y et phi) réelle de sorte que Robotino se déplace de la position réelle à la position de consigne avec une vitesse variable définie dans l'interface de ce bloc.

De ce bloc, il y a aussi 3 autres sorties qui sont :

- Position atteinte : dès que les sorties vx et vy délivrent 0, la position de destination est considérée atteinte et la sortie délivre un signal vrai.

- Orientation atteinte : dès que la sortie omega délivre 0, l'orientation de destination est considérée atteinte et la sortie délivre un signal vrai.

- Pose atteinte : la sortie délivre un signal vrai si à la fois la position et l'orientation de destination sont atteintes. Sinon faux.

Hors jusqu'à présent, le programme passait d'une position à une autre une autre quand la variable de sorties Position atteinte était vrai, c'est-à-dire que la valeur de consigne et celle réelle sont égales pour x et y en négligeant phi. C'est pourquoi, le programme a été changé pour qu'il passe d'une position à une autre une autre quand la variable de sorties Pose atteinte était vrai, pour ne plus négliger phi.

Comme cela le programme permettait de mesurer les trajectoires utilisant la variable phi et aussi de refaire les mesures de celles ne l'utilisant pas faites à la séance précédente pour éviter toutes erreurs.

2 Décembre 2013

Pour avoir un résultat réellement comparable, car jusqu'à présent les mesures prenaient les valeurs obtenues par odométrie comme référence, alors qu'elle présente déjà une certaine incertitude.

Pour cela, après discutions avec Mr Rochdi MERZOUKI, le choix a été de délimité un rectangle selon X et selon Y avec des rotation de 90° à chaque angle.

Le principe était de prendre un rectangle marqué au sol dans l'espace de navigation de la salle Robotino, de définir le parcours pour que le Robotino l'effectue d'abord en le commandant avec l'odométrie, puis avec Northstar.

Pour répondre à ce problème : écriture de 3 sous programme :

un sous programme nommé Northstar_pgr_enregistr inspiré du sous programme nommé Northstar_pgr auquel se rajoute l'enregistrement des valeur de x, y et phi.

un sous programme nommé Odometrie_pgr_enregistr inspiré du sous programme nommé Odometrie_consig_Northstar_enregistr ne gardant que la partie qui attrait à l'Odométrie

3 Décembre 2013

Etude d'un programme de contrôle de trajectoire du Robotino sous Matlab écrit par Achille, un doctorant.

Recherches et compréhension des fonctions liées au module Northstar, figurant dans la toolbox RobotinoMatlab.

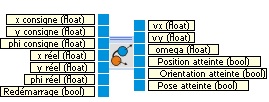
Ecriture d'un programme Matlab nommé Northstar.m qui reprend les entrées et sorties du bloc Northstar sur RobotinoView2.

4 Décembre 2013

Test du sous programme nommé Odometrie_pgr_enregistr sur un parcours rectangulaire mais problème d'enregistrement du parcours en entier car ce sous programme est combiné avec un autre sous programme qui s'occupe de l'incrémentation de position et l'enregistrement est remis à zéro des que l'on change de sous programme. Le problème est le même avec le sous programme Northstar_pgr_enregistr. Les pistes envisagées sont d'utiliser une variable globale mais toujours le problème entre les 2 sous programme, autre piste, fusionné les 2 sous programme.

L'autre problème soulevé par le sous programme Northstar_pgr_enregistr est que avec le bloc nommé Parcoureur de position, on passe maintenant d'une position à une autre quand Pose atteinte est vrai, c'est-à-dire la valeur de X, de Y et de Phi en consigne et mesurée par Northstar doivent être égale. Ce qui semble très difficile.

5 Décembre 2013

Modification du sous programme Northstar_pgr_enregistr pour ne plus utilisé la variable Pose atteinte mais une comparaison avec un Delta.

9 Décembre 2013

Modifications du programme Matlab nommé Analyse_Sorties.m, pour qu'il calcule la distance entre le courbes et enfin déterminer :

- l'écart moyen

- l'écart minimum

- l'écart maximum

Modifications du programme Matlab nommé Northstar.m, en s’inspirant des précédentes modifications pour calculer la distance entre les valeurs réelles et les valeurs de consignes et déterminer les valeurs de vitesse en conséquence.

Modifications des programmes Matlab nommé Analyse_Sorties.m et nommé Northstar.m, car l'utilisation de la fonction dist sur Matlab qui correspond à une fonction de pondération de la distance Euclidienne, fonctionne sur la version de Matlab de mon PC. Le programme a été modifié sur ce PC car la salle Robotino était occupé par un TP le matin. Et lors des testes l'après-midi, aucune version de Matlab sur les PC de la salle Robotino ne connait cette fonction, donc changement avec des if et else.

12 Décembre 2013

Compilation du programme Matlab nommé Northstar.m, 2 messages d'erreurs :

  Error using ==> loadlibrary at 282
  Microsoft Visual C++ 2005 or 2008 is required to use this feature.

  Error in ==> init at 20
  loadlibrary( 'rec_robotino_com_c.dll', 'Com.h')

La première erreur est dû à la version de Microsoft Visual C++.

La deuxième est dû à l'oubli du lancement du fichier Matlab nommé Startup.m qui compile les librairies des fonctions des blocs RobotinoView2 avec Matlab.

Compilation du même programme sur un autre PC, pas d'erreur de compilation mais que des valeurs nulles alors teste un programme sur RobotinoView2 et donc découverte que le réseau Robotino n'était pas configuré sur ce PC.

Compilation du même programme sur un troisième PC, pas d'erreur de compilation ni de réseau, mais les valeurs obtenues ne semblent pas cohérentes.

16 Décembre 2013

Modifications du programme Matlab nommé Northstar.m, pour obtenir des valeurs cohérentes.

Récupérations d'images, d'imprimes écran et de valeurs pour compléter le rapport intermédiaire et le PowerPoint associé.

19 Décembre 2013

Soutenances intermédiaires de projets

Semaines de modules transversaux : du 6 au 10 Janvier 2014, du 13 au 17 Janvier 2014, du 20 au 24 Janvier 2014

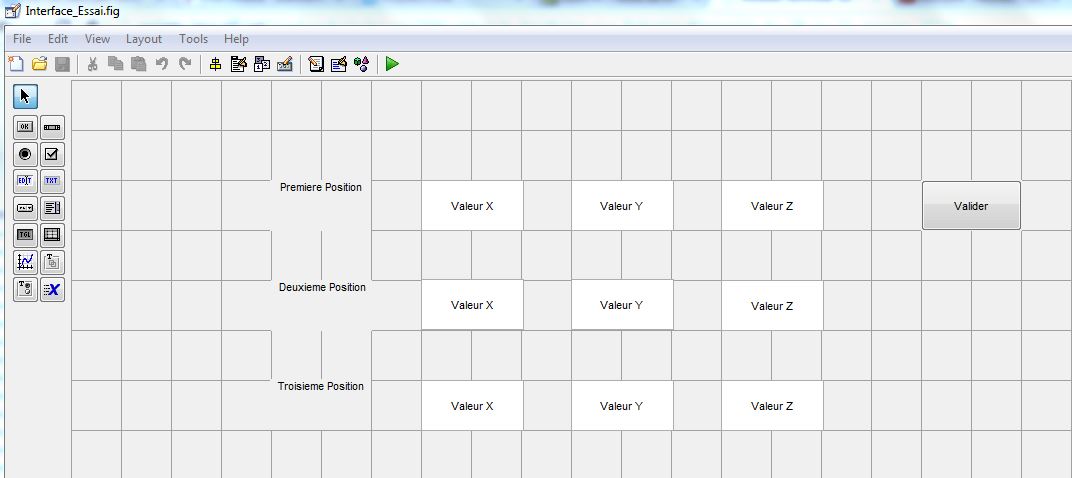
Programmation d'une interface graphique sur Matlab appelé GUI (Graphical User Interfaces) avec un fichier nommé Interface_Essai.fig :

Export au format script nommé Interface_Essai.m

Ajout de code pour traitement

  global g_x1;

Cette instruction déclare la variable g_x1 en globale

  g_x1 = str2num(get(handles.x1,'string'));

Cette instruction définit g_x1 égale la valeur de l'edit text x1

L'instruction handles sert à définir l'utilisation d'un Tag

L'instruction get retourne la valeur de propriété spécifique de l'objet graphique avec des poignées

L'instruction str2num convertie un char (string) en nombre (double)

  assignin('base','x1',g_x1);

Cette instruction définit la variable x1 dans le Workspace et lui attribut la valeur de g_x1

Les mêmes instructions sont définit pour g_x2, g_x3, g_y1, g_y2, g_y3, g_z1, g_z2 et g_z3

Semaine du 28 au 31 Janvier 2014

Création d'un programme Northstar_startup.m qui redéfinit le chemin pour atteindre les répertoires blockset et toolbox

   addpath('C:\Documents\Cours Polytech\Semestre 9\PFE\Didactic\RobotinoMatlab\blockset');
   addpath('C:\Documents\Cours Polytech\Semestre 9\PFE\Didactic\RobotinoMatlab\toolbox');

Création d'un programme Northstar_param_dichotomie.m

fonction principale :

   a = calib_min;
   b = calib_max;
   
   c = (a+b)/2;
   iter=0
   
   while norm(func(c))>=epsi && iter<nb_it_max
   
       if x_N_c == x_O_c && y_N_c == y_O_c && z_N_c == z_O_c
           calib_final = c;
       end
       
       if abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) && abs(y_N_c-x_N_a) < abs(y_N_c-x_N_b) || ...
       abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) && abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) || ...
       abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b) && abs(x_N_c-x_N_a) < abs(x_N_c-x_N_b)
       
           b=c;
           c=(a+c)/2;
       else
           a=c;
           c=(b+c)/2;
       end
       
       iter=iter+1;
   
   end
   
   calib_final = c;

Semaine du 4 au 7 Février 2014

Erreurs de compilation fichier init.m

 Warning: Name is nonexistent or not a directory: \bin\x64. 
 > In path at 110
 In init at 20
 Warning: Name is nonexistent or not a directory: \include\rec\robotino\com\c. 
 > In path at 110
 In init at 21
 ??? Error using ==> loadlibrary>lFullPath at 613
 Could not find file Com.h.

 Error in ==> loadlibrary at 226
       header=lFullPath(header);

 Error in ==> init at 22
   loadlibrary( 'rec_robotino_com_c.dll', 'Com.h', …

Correction du fichier init.m

code initial :

  robotinoMatlabDir = getenv('ROBOTINOMATLAB_DIR');
  robotinoMatlabINC1 = strcat( robotinoMatlabDir, '\include\rec\robotino\com\c' );
  robotinoMatlabINC2 = strcat( robotinoMatlabDir, '\include' );

modification :

  robotinoMatlabDir = 'C:\Program files\Didactic\RobotinoMatlab';
  robotinoMatlabINC1 = 'C:\Program files\Didactic\RobotinoMatlab\include\rec\robotino\com\c';
  robotinoMatlabINC2 = 'C:\Program files\Didactic\RobotinoMatlab\include';

Toujours 2 messages d'erreurs

  Error using ==> loadlibrary at 282
  Microsoft Visual C++ 2005 or 2008 is required to use this feature.

  Error in ==> init at 20
  loadlibrary( 'rec_robotino_com_c.dll', 'Com.h')

Utilisation de l'instruction : >> mex -setup , qui permet de définir le compilateur

Les fonctions Matlab écrits en C + + sont appelés MEX-files. MEX signifie Matlab EXectuable. Les MEX-files sont liés de façon dynamique sous-programmes produits à partir de C / C + + ou Fortran. Ces fichiers contiennent des extension .dll. La principale raison d'écrire un MEX-file est d'utiliser C pré-existant / C++ ou Fortran routines Matlab sans avoir à les recoder.

 Welcome to mex -setup.  This utility will help you set up  
 a default compiler.  For a list of supported compilers, see  
 http://www.mathworks.com/support/compilers/R2011a/win64.html 

 Please choose your compiler for building MEX-files: 

 Would you like mex to locate installed compilers [y]/n? y

 Select a compiler:
 [1] Microsoft Visual C++ 2005 SP1 
 [2] Microsoft Visual C++ 2010 

 [0] None 

 Compiler: 0

 mex: No compiler selected. No action taken. 

 Warning: The MATLAB C and Fortran API has changed to support MATLAB 
          variables with more than 2^32-1 elements.  In the near future 
          you will be required to update your code to utilize the new 
          API. You can find more information about this at: 
          http://www.mathworks.com/support/solutions/en/data/1-5C27B9/?solution=1-5C27B9 
          Building with the -largeArrayDims option enables the new API.

Solutions envisagées :

Désinstallation puis réinstallation dans cette ordre avec teste entre chaque de :

- Microsoft Visual Studio 8

- Microsoft Visual Studio 9

- Microsoft Visual Studio 10

- Microsoft Visual C++ 2005

- Microsoft Visual C++ 2008

- Microsoft Visual C++ 2010

Puis en parlant avec un doctorant travaillant aussi sur Matlab, qui m'a dit que le problème venait du PC sur lequel était compilé les programmes.

Car c'est un PC 64 bits et que Matlab ne fonctionne pas de la même façon sur un PC 32 bits et 64 bits.

En cherchant ensemble sur internet, apparemment ça serait un problème de librairie mais sans savoir laquelle il m'a proposé la solution qu'il a utilisé lors d'une démonstration pour l'université : c'est de faire une partition du PC avec :

- une partition de Windows 7 en 64 bits

- une partition de Windows 7 en 32 bits

Mais avant de faire ça sur un PC, j'ai vérifié et il y a 2 PCs 64 bits et 2 PCs 32 bits.

Donc à partir de ce moment, la compilation se fait sur Matlab sur un PC 32 bit.

Semaine du 10 au 14 Février 2014

Modifications du programme Northstar.m pour imbriquer les conditions d'utilisation des valeurs obtenues par le capteur Nothstar et voir d'où venait les erreurs si c'était le cas

4 conditions :

(1) S’il n’y a aucune détection du capteur C’est-à-dire s’il ne capte aucun spot lumineux et que leurs intensités sont nuls

  if ( NorthStar_magSpot0(NorthStarId) ~= 0 && NorthStar_magSpot1(NorthStarId) ~= 0 ...
    && NorthStar_numSpotsVisible(NorthStarId) ~= 0)

(2) Si la détection est trop faible C’est-à-dire si le capteur capte les 2 spots lumineux et que chacun d’eux une intensité supérieur à un pourcentage, ici 3 %

  if (NorthStar_magSpot0(NorthStarId)/1000 > 3 && NorthStar_magSpot1(NorthStarId)/1000 > 3 ...
   && NorthStar_numSpotsVisible(NorthStarId) == 2)

(3) Si les valeurs du capteur Northstar semblent incohérentes C’est-à-dire si pour une vitesse non nulle selon x, y ou phi, la valeur de la position ne doit pas être égale à 0

  if (Vx~=0 || Vy~=0 || Vphi~=0) && ...
       (Nx~=0 && Ny~=0 && Nphi~=0)

(4) Si l’écart entre les valeurs de l’Odométrie et celles de Northstar sont assez importantes C’est-à-dire si l’erreur entre la valeur du capteur Northstar et celle par Odométrie pour chaque variable x, y et phi est supérieur à la variable erreur_O_N qui est la valeur d‘erreur acceptable vis-à-vis de la précision du capteur Northstar

  if (abs(Ox - Nx) > erreur_O_N && abs(Oy - Ny) > erreur_O_N ...
   || abs(Ox - Nx) > erreur_O_N && abs(Ophi - Nphi) > erreur_O_N ...
   || abs(Oy - Ny) > erreur_O_N && abs(Ophi - Nphi) > erreur_O_N)

Si ces 4 conditions sont remplies les valeurs utilisées sont celles du capteur Northstar

  x = Nx;
  y = Ny;
  phi = Nphi;

Sinon ceux sont celles obtenues par le capteur par Odométrie

  x = Ox;
  y = Oy;
  phi = Ophi;

La condition la plus gênante était d'avoir des valeurs aberrantes : le problème était d'abord de savoir sous quelles conditions, on peut les considérer aberrantes et quelle peut être l'origine.

Semaine du 17 au 21 Février 2014

Programme par dichotomie

4 conditions :

(1) Si la valeur par Odométrie de x, y et phi est dans l’intervalle [a, c] des valeurs de Northstar

  if (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc) && (phiNa <= phiO && phiO <= phiNc)

(2) Si la valeur par Odométrie de x, y et phi est dans l’intervalle [c, b] des valeurs de Northstar

  elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb) && (phiNc <= phiO && phiO <= phiNb)

(3) Si la valeur par Odométrie de x et y (en négligeant une erreur sur phi) est dans l’intervalle [a, c] des valeurs de Northstar

  elseif (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc)

(4) Si la valeur par Odométrie de x et y (en négligeant une erreur sur phi) est dans l’intervalle [c, b] des valeurs de Northstar

  elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb)

Si les valeurs sont dans l'intervalle de calibration [a, c]

  b=c;
  c=(a+c)/2;

Si les valeurs sont dans l'intervalle de calibration [c, b]

  a=c;
  c=(b+c)/2;

Première Modification :

Changement de un seul epsilon epsi mais dans un second temps, il en utilisait deux, un pour les valeurs en millimètre (x et y) : epsi_mm et un pour les valeurs en degrés (phi) : epsi_deg.

Avant modification :

  (abs(xNc - xO)>=epsi || abs(yNc - yO)>=epsi || abs(phiNc - phiO)>=epsi)

Après :

  (abs(xNc - xO)>=epsi_mm || abs(yNc - yO)>=epsi_mm || abs(phiNc - phiO)>=epsi_deg)

Seconde Modification :

Au lieu de regardé si les valeurs sont dans l'intervalles de calibration [a, c] ou [c, b], le programme cherche si les valeurs sont inférieur ou supérieur avec la calibration de c :

Avant modification :

  if (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc) && (phiNa <= phiO && phiO <= phiNc)
  elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb) && (phiNc <= phiO && phiO <= phiNb)
  elseif (xNa <= xO && xO <= xNc) && (yNa <= yO && yO <= yNc)
  elseif (xNc <= xO && xO <= xNb) && (yNc <= yO && yO <= yNb)

Après :

  if xO <= xNc && yO <= yNc && phiO <= phiNc)
  elseif xNc <= xO && yNc <= yO && phiNc <= phiO
  elseif xO <= xNc && yO <= yNc)
  elseif xNc <= xO && yNc <= yO

Programme pas à pas

Le programme de dichotomie ayant toujours des défauts de recherches

Création d'un autre programme pas à pas, même principe que la dichotomie, mais il balaye tout l'intervalle de calibration.

D’abord pour trouver les extrêmes de l'intervalle de départ de recherche du programme par dichotomie, c'est-à-dire les valeurs (x, y et phi) du capteur Northstar sont différentes de 0.

Puis pour trouver l'intervalle dans lequel devrait se trouver le résultat de la recherche par dichotomie, c'est-à-dire si la différence entre les valeurs (x, y et phi) du capteur Northstar et celles de l’Odométrie sont inférieurs aux valeurs epsi_mm et epsi_deg, utilisées dans l’algorithme de dichotomie.

24 Février 2014

Mise à jour des Gantt

Travail sur le rapport et le Wiki

25 Février 2014

Rendu du Rapport final de projet

26 Février 2014

Travail PowerPoint pour la soutenance

27 Février 2014

Soutenances finales de projets

Résultats

Sur RobotinoView

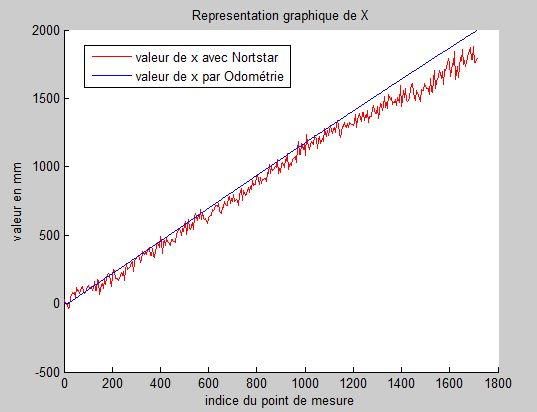
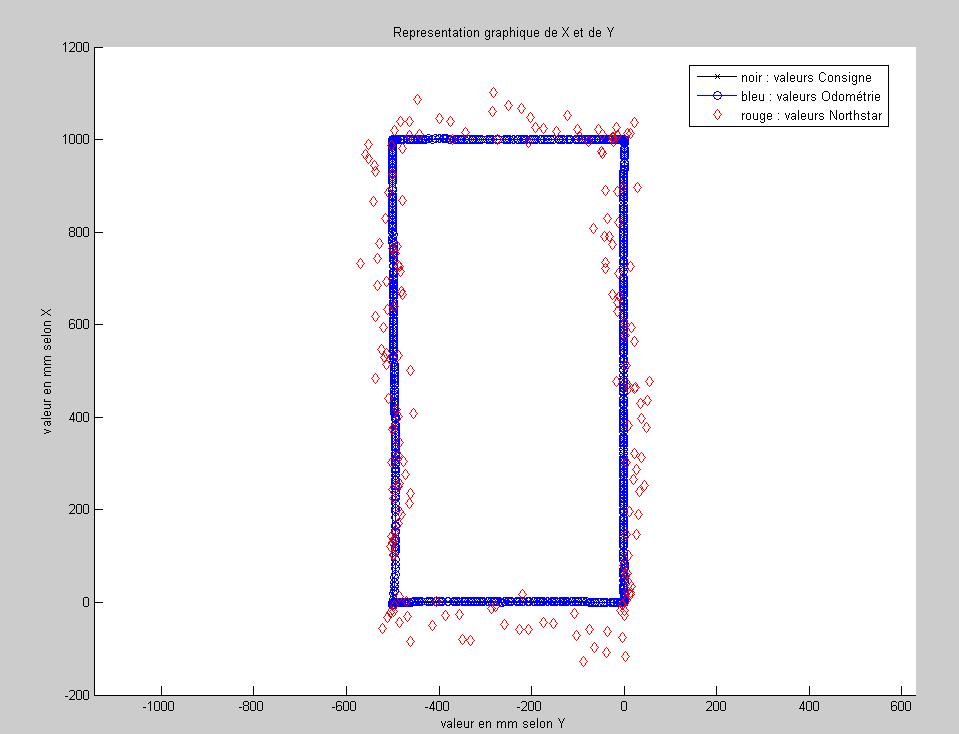
Parcours d’un rectangle de 1 m sur 50 cm :

Ces graphiques montrent que l'on a un écart maximum de 10 cm or dans la documentation, il est dit que le capteur Northstar a une précision de +/- 5 cm; ce qui correspond

Sur Matlab

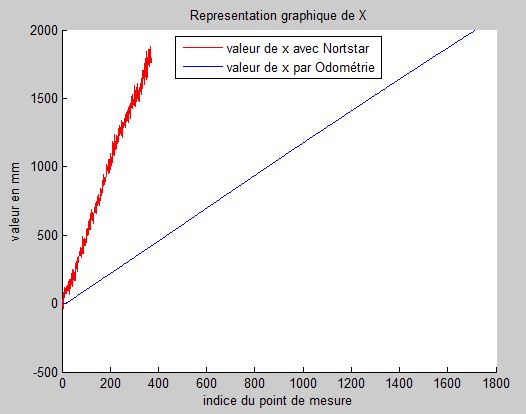
Pour le même parcours

Sur le graphique de gauche on voit que les valeurs de Northstar sont de 2 à plus 100 fois plus grandes c'est-à-dire jusqu’à quelques mètres d'erreurs.

Alors que sur le graphique de droite, on voit un zoom sur les valeurs de consigne qui permet de voir que les valeurs par Odométrie sont aussi précises.

Gestion de projet

Planning prévisionnel

Planning prévisionnel sous forme de Gantt fixé au début du projet et refixé à partir de la soutenance intermédiaire :

Ce Gantt fait au début des deux parties du projet devait me servir de fil conducteur pour estimer ma progression et mon retard si cela était le cas.

Planning réel

Planning réel sous forme de Gantt pour voir à quoi est dû l'écart entre le planning prévisionnel et réel :

Les points non suivis :

- Durée des temps de recherches plus court

- Durée des temps de prise en mains plus court

Les points non ou mal évalués :

- Temps de programmation sur RobotinoView et Matlab (trop court car déjà utilisé mais points complètement nouveaux)

- Temps perdu lié à la compatibilité des logiciels ou des librairies et mise à jour

Les points ajoutés :

- Programmation de l’analyse avec Matlab des résultats

- Teste d'autres modes de recherche de paramétrage (en premier abord la dichotomie devait suffire)

- Programmation interface graphique GUI Matlab

Rapport

Fichier:Rapport PFE Lenormand Mathieu.pdf

Annexes

Ordinogramme du programme Northstar sur Matlab