IMA4 2016/2017 P47

Cahier des charges

Présentation générale du projet P47 :

Contexte et Description

La modélisation des systèmes est indispensable dans beaucoup de domaines: automobile, aéronautique, robotique, etc. Elle permet d'obtenir un modèle mathématique des systèmes pour réaliser leur commande, comprendre leur fonctionnement et surveiller leur bon fonctionnement afin de pouvoir apporter des actions correctives en temps réel lors d'un défaut ou d'une défaillance du systèmes. Cette modélisation peut être réaliser en se basant sur les lois physiques (boites blanches) ou en utilisant les données (boîtes noires).

Ce projet a pour but la modélisation d’un robot à trois roues omnidirectionnelles à savoir le Robotino. Cette modélisation se fera à partir des données recueillies sur ce robot. Ce projet se déroulera suivant les phases suivantes :

Estimer un modèle mathématique d'un robot mobile.
Déterminer le modèle à partir de mesures recueillies par le robot.
Valider le modèle avec d'autres mesures qui n'ont pas servi à déterminer celui-ci.
Tester en ligne le modèle.

La validation consistera à comparer le comportement du modèle à celui du robot en appliquant les mêmes commandes aux deux.

Objectif du projet

Obtenir le modèle mathématique du Robot pour avoir les positions en x et y avec un mouvement en lacet et les vitesses selon les axes

Choix techniques (matériel et logiciel)

Algorithme d'optimisation non linéaire.
Méthode d'identification des sous-espaces.
Matlab: Toolbox identification, outil direct.
Robotino
PC equipé d'une carte réseau afin d'utiliser le Robotino en Wifi ou avec un câble Ethernet.

Liste des tâches à effectuer

Prise en main du Robotino.
Prise en main de la Toolbox Identification de Matlab.
Prise en main de la Toolbox optimisation non linéaire de Matlab.
Identification boite noire d’un modèle linéaire du système :
- étude des méthodes d’identification des sous-espaces ;
- application à l’identification du robot.
Identification boîte noire d’un modèle non linéaire du robot :
- étude des méthodes d’optimisation non linéaires ;
- application à l’identification du robot.
Validation du modèle

Feuille d'heures

Tâche	Prélude	Heures S1	Heures S2	Heures S3	Heures S4	Heures S5	Heures S6	Heures S7	Heures S8	Heures S9	Heures S10	Heures supplémentaire	Total
Définition cahier des charges	3				1	1							5
Rédaction Wiki		1	1	1	1	1						5	10
Recherche		6	5	7	2	1	1						22
Campagne d'acquisition		2	5		2							2	11
Simulation: Initiation à l'identification d'un modèle						4	6						10
Simulation: Identification du modèle linéaire d'un robot mobile								6	6	8	6	10	36
Validation du modèle linéaire en ligne												12	12

Avancement du Projet

Semaine 1

Lundi 16-18h :

Nous étions en réunion en D304B avec Mr Pekpe, et nous avons discuté des points fondamentaux du travail qu'on doit effectuer, et qui consistent au début à aborder le Robotino d'une façon linéaire c'est-à-dire par rapport au repère lié à son centre, et dans une seconde étape essayer d'aborder le Robotino mais d'une façon non linéaire cette fois ci par projection sur un repère fixe.

Pour les deux points on a vu des documents avec Mr Pekpe qui expliquent comment les équations d'un Robotino à trois roues mobiles peuvent être déduites, et on a vu que pour ces modèles les équations se résument à des écritures matricielles en général sous la forme :

                                                                       X' = AX + BU
                                                                       Y  = CX + DU

Où :

X la variable de l'état (vitesse théorique des moteurs)
U la variable de la commande (vitesse suivant les axes)
Y la mesure ou la sortie (vitesse réelle)
A la matrice de dynamique
B la matrice de commande
C la matrice d'observabilité
D la matrice d'action directe

Mercredi 14-18h :

Nous avons fait la prise en main du logiciel Robotinoview, en commençant par regarder toutes les fonctions disponibles sur le logiciel, et en soulignant celles qui seront utiles pour notre projet.

Nous avons appris à réaliser une campagne d'acquisition des paramètres X, Y, U (déjà traité théoriquement ci-dessus) et la position P qui renvoie l'évolution de notre robot en déplacement sans frottements.Cette campagne a été réalisé avec le logiciel Robotinoview et ses données ont été traité sur Matlab.L’intérêt de Matlab est de stocker les données et de pouvoir les tracer pour bien interpréter les résultats en graphe.

Ensuite nous avons fait des recherches sur les documents qui nous ont été fourni par notre encadrant, sur les étapes mathématiques qui déterminent le modèle linéaire du Robotino.

Jeudi 8-10h :

Nous avons continué nos recherches sur les documentations fournies.

Semaine 2

Lundi 16-18h :

Nous avons continué nos recherches sur la documentation fournie.

Mercredi 14-19h :

Aujourd'hui, nous avons fait une campagne d'acquisition sur Matlab et une sur RobotinoView afin de relever les différences entres ces deux logiciels et de déterminer lequel convient le plus pour notre méthode qui vise la modélisation linéaire du Robotino. Nous avons constaté que nous obtenons beaucoup plus de données sur la position du Robot sur Matlab que sur RobotinoView. Pour vous donner un ordre de grandeur sur une période de 30 minutes, nous obtenons environ 2000 données sur RobotinoView alors que sur Matlab nous en obtenons à peu près 300 000. Ce qui nous montre bien l'intérêt d'utiliser Matlab pour nos campagnes d'acquisitions qui nous donnera un modèle beaucoup plus précis car plus nous avons de données et plus on s'approche de la courbe théorique.

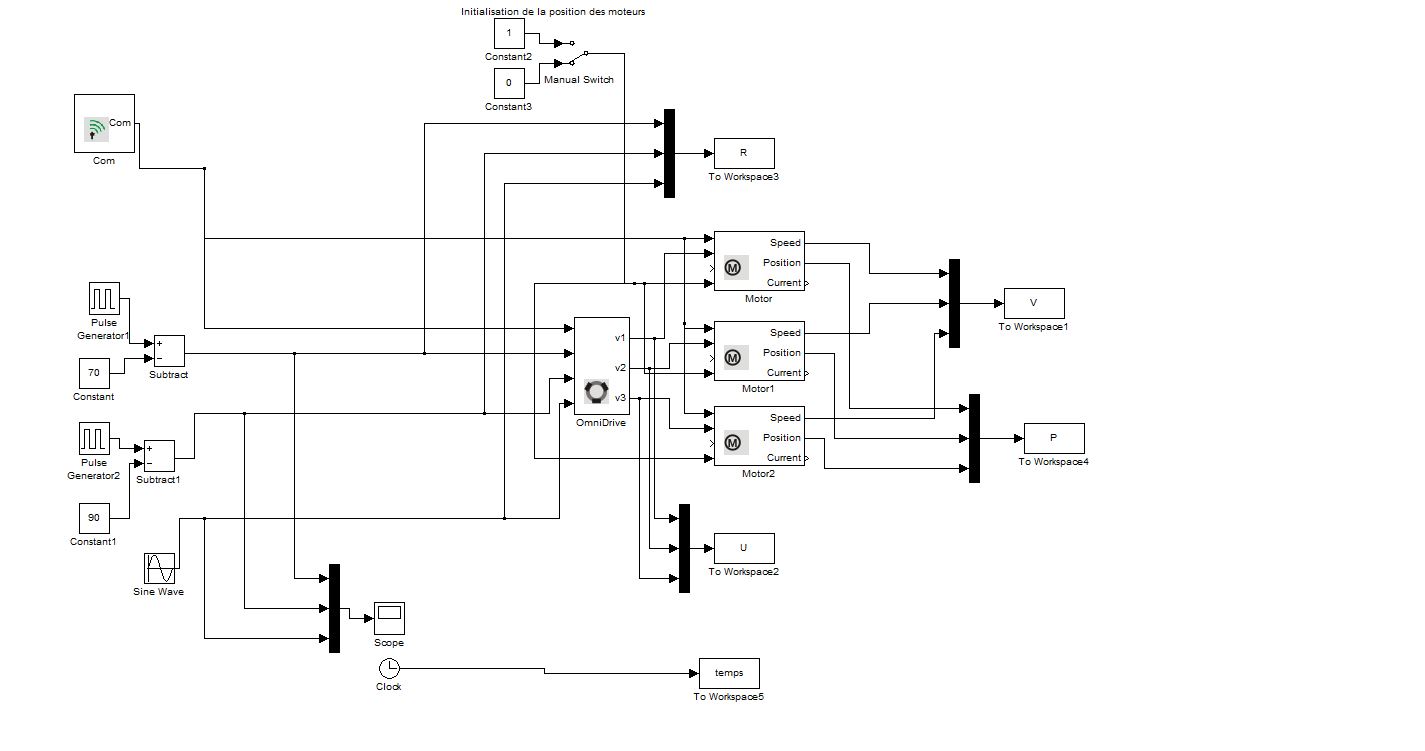
- Sous-programme permettant la commande du Robot sur un temps choisi avec consignes variables ainsi que l'enregistrement des données voulues:

- Programme principal sur 6 steps avec des consignes respectives à chaque step, réalisé en boucle 100 fois :

- Traduction du programme déjà cité mais à présent sur Matlab, on voit qu'avec l'option "inf" (temps infini) on obtient plus de données :

Jeudi 11-14h :

Discussion avec M.PEKPE sur l'avancement de notre projet et la lecture d'une partie sur la méthode d'identification des sous-espaces sur les nouveaux documents fournis.

Semaine 3

Le but de la documentation est de comprendre que pour déterminer les défauts d'un système, il faut comparer son comportement au modèle mathématique. La différence entre le comportement du système et celui du modèle mathématique est exprimé sous forme d'un résidu. Pour l'obtention du modèle mathématique utilisé, on utilise les méthodes d'identification pour caractériser le modèle de bon fonctionnement du système.

Lundi 16-18h : ( Méthodes classiques des sous-espaces )
- Formulation du problème :

On considère un système linéaire :

X(k+1)=A.X(k)+B.U(k)
Y(k)  =C.X(k)+D.U(k)

comme noté auparavant. L'objectif est de déterminer les matrices A,B,C et D du système à partir des seules données qu'on a sur les entrées et les sorties u et y. On peut aussi chercher à résoudre le système en déterminant les matrices T^−1.A.T, T^−1.B, C.T et D.Et donc on peut écrire le système d'une nouvelle façon comme suit :

X(k+1)=T^−1.A.T.X(k)+T^−1.B.U(k)
Y(k)  =C.T.X(k)+D.U(k)

- Matrices du système :

Les matrices de ce système est leur types sont définies de la façon suivante: La matrice de Hankel d'entrée Ui et la matrice de Hankel de sortie Yi.Avec ces deux matrices on définit bien la matrice de Hankel des mesures T=(Y U).

Mercredi 13-18h :
- Identification du système :

Pour identifier un système suivant les méthodes des sous-espaces, il faut d'abord estimer la matrice d'observabilité (qui détermine le rang de notre matrice globale), ensuite au moment où on arrive à estimer la matrice d'observabilité on peut commencer à réfléchir sur la réalisation du système, c'est-à-dire, déterminer les paramètres T^−1.A.T, T^−1.B, C.T et D.

Semaine 4

Lundi 16-18h

On a lu les documents pour la partie théorique de notre projet sur les méthodes des sous-espaces.

Mercredi 14-18h:

Documentation sur les méthodes des sous-espaces, et préparation pour pouvoir expliquer à Mr. Pekpe ce que nous avons compris.

Jeudi 8-10h:

Passage oral et écrit sur le tableau devant Mr Pekpe pour qu'il évalue si on a bien compris la théorie.

Semaine 5

Lundi 16-18h:

On a essayé de traiter un exercice plus simple qu'on a vu en TD suite à la demande de Mr. Pekpe. Tout d'abord on a essayé de nous familiariser avec Matlab et MatlabSimulink, en regardant les fonctions qui peuvent nous être utiles.

Mercredi 14-18h:

On a pu simuler l'exercice que le mercredi vu qu'il fallait qu'on se familiarise avec les logiciels, mais on a réussi à traiter un autre exercice plus compliqué dans les deux dernières heures de la séance.

Semaine 6

Cette semaine nous avons continué nos identifications des modèles sur des systèmes vus en cours afin d'améliorer notre compréhension et nos connaissances sur les méthodes des sous-espaces employées. Pour ce qui est de l'identification du robot mobile Robotino on compte l'entamer dès la semaine prochaine.

Semaine 7

Nous avons rencontré Mr. Pekpe afin de pouvoir commencer l'identification du robot mobile.Tout d'abord avec la méthode de résolution des sous-espaces n4sid(Algorithmes de sous-espace pour l'identification de systèmes stochastiques déterministes combinés), nous avons mis au point un script sur Matlab pour déterminer notre modèle.Nous avons utilisé des données recueillies lors des campagnes d'acquisitions, où on a utilisé la position sur l'axe lacet comme sortie du système avec une entrée dite MISO (miltuple input single output).

Semaine 8

Au cours de cette semaine, nous avons réussi à déterminer le modèle du Robotino avec la position sur l'axe lacet. Nous avons validé le modèle obtenu avec les données recueillies lors des campagnes d'acquisitions. Nous voyons que les positions réelles collent avec les positions estimées par le modèle jusqu’à un tiers du temps. Il est normal qu'au bout d'un moment le modèle diverge de la réalité au bout d'un certain temps, il faudrait ajouter un observateur et faire un retour d'état pour s'assurer que notre modèle colle parfaitement avec les données réelles même pendant une très longue durée.

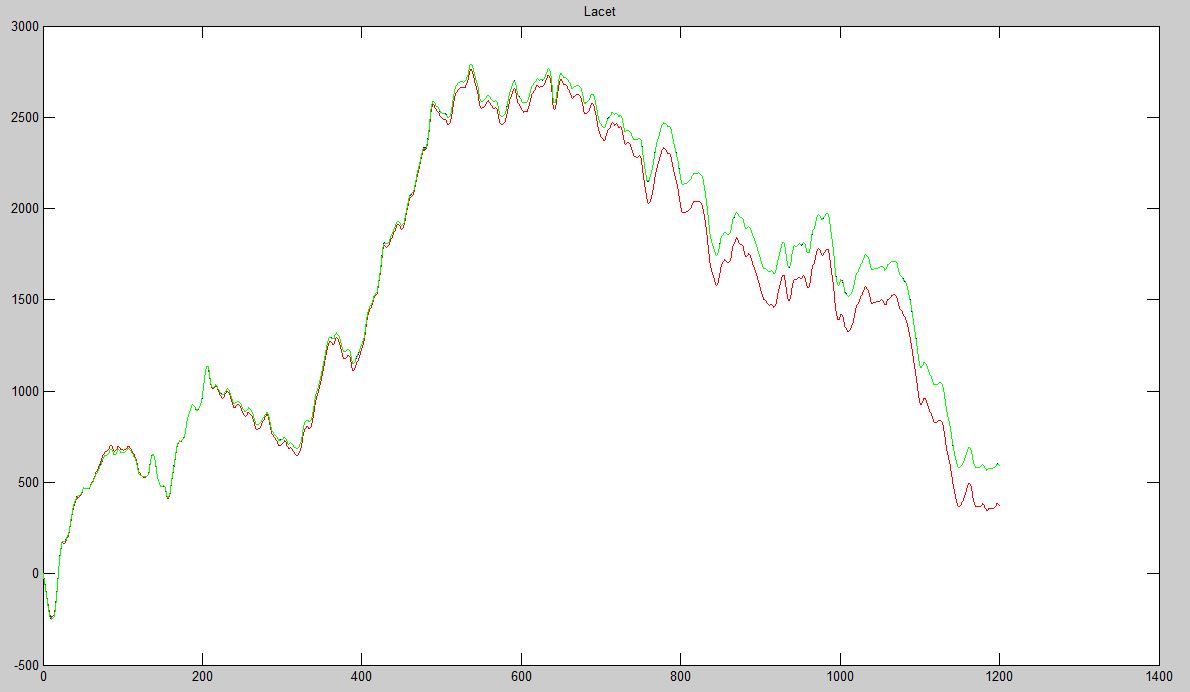
Et voici le graphe de la position du robot en lacet exprimé en tours en fonction du temps exprimé en secondes que nous retrouvons :

Nous avons en vert la position réelle du robot et en rouge la position estimée par le modèle obtenu.

Semaine 9

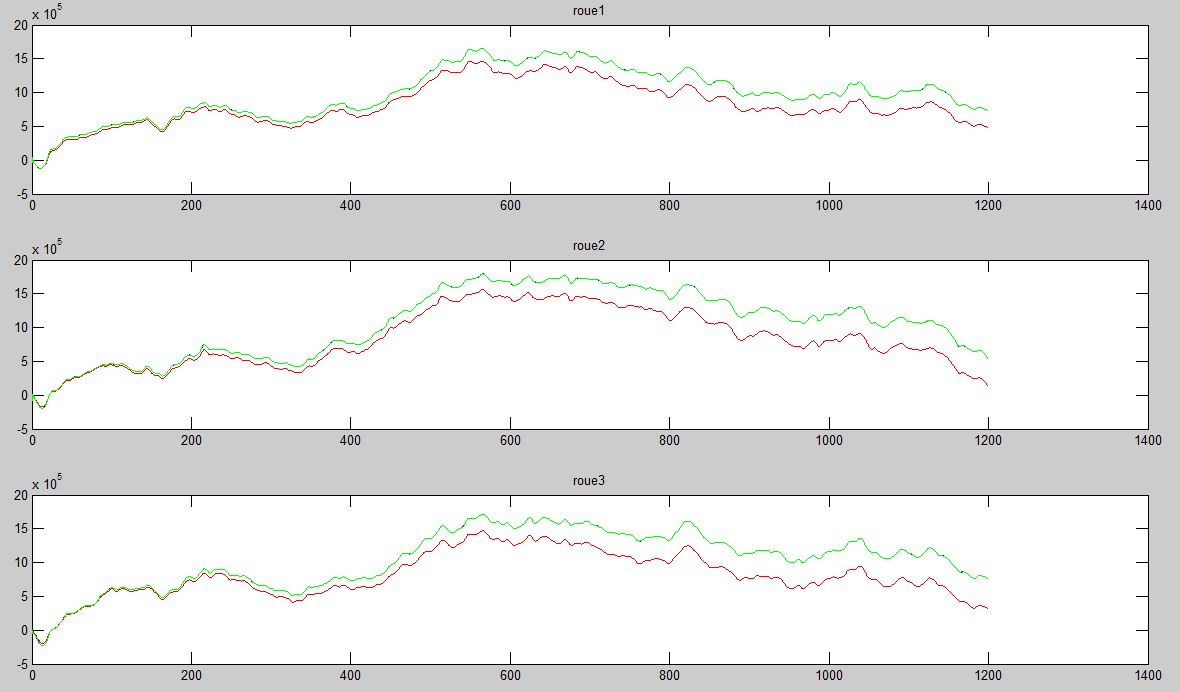
Nous réalisons cette semaine le modèle du Robotino pour les positions angulaires des roues θ1, θ2 et θ3. Nous avons réutilisé le script réalisé pour le modèle précédent et nous l'avons modifié car nous sommes plus dans un système MISO mais dans un système à multiples sorties à présent, c'est-à-dire MIMO. Nous avons rencontré plusieurs difficultés lors de la modification de notre code. Nous avons demandé de l'aide à Mr. Pekpe et il nous a aiguillé sur les modifications à réalisé. Nous avons réussi à obtenir le modèle pour les positions angulaires des roues. Comme pour le précédent, nous l'avons validé hors-ligne.

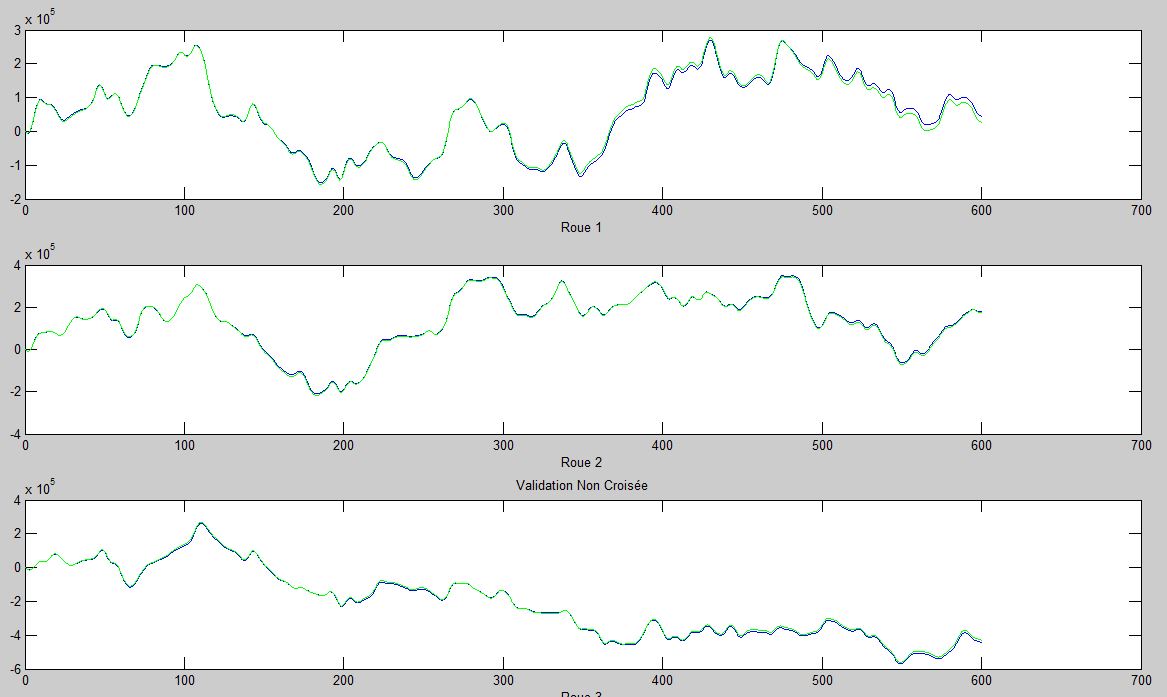
on peut remarquer l'évolution de la position des roues sur le premier tiers des données recueillies qui ont servies à faire le modèle (validation non croisée). La position réelle des roues en vert suit plutôt bien, où sur l'axe des ordonnés le nombre de tours des roues en fonction du temps.

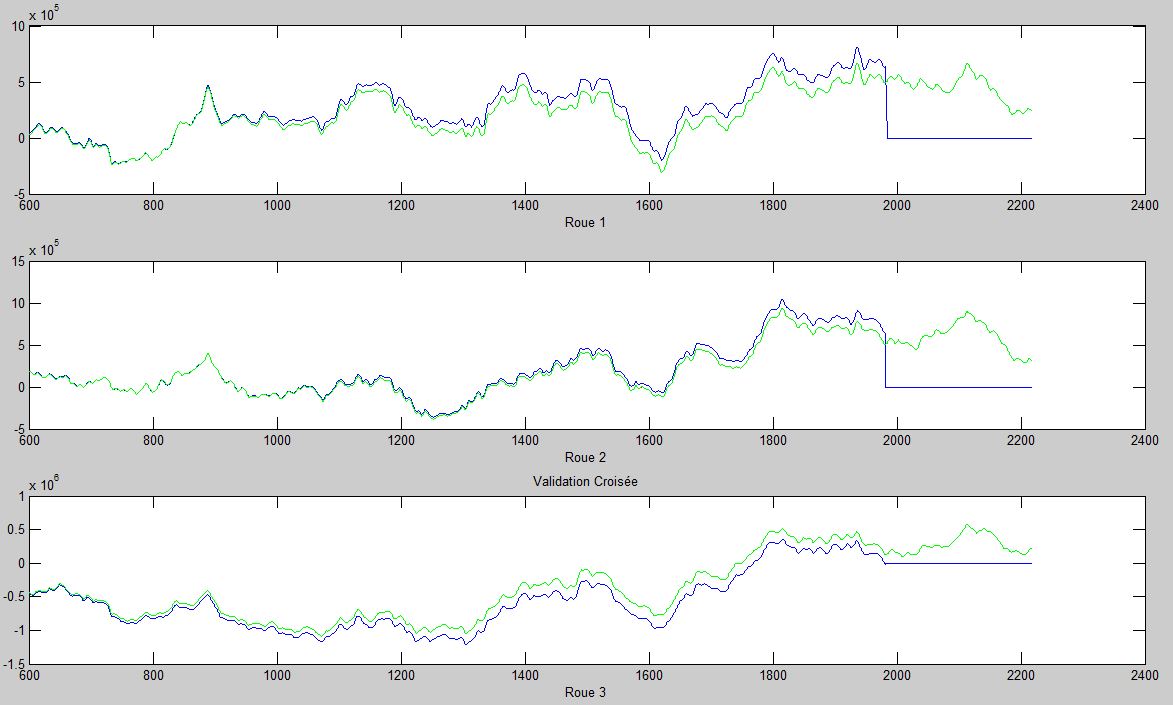
Pour les deux tiers restants des données qui n'ont pas servies à faire le modèle (validation croisée), on remarque que la position des roues réelles en vert diverge à partir d'un certain moment, ce qui est normal vu que tout système diverge de son modèle.

Semaine 10

La semaine précédente,nous avons donc réalisé nos premiers objectifs qui étaient de déterminer un modèle mathématique d'un robot mobile à partir de mesures recueillies par le robot et de valider ce modèle en mode hors-ligne. A présent, nous allons faire en sorte de valider ces 2 modèles obtenues en ligne, c'est-à-dire que nous devons comparer le comportement du modèle à celui du robot en appliquant les mêmes commandes aux deux. Il ne faut pas oublier que pour l'instant nous travaillons en roues libres et donc qu'il n'y a aucune force de frottements s'appliquant au robot. Si le temps nous le permet et que nous avons validé nos deux modèles en ligne alors nous estimerons un modèle non linéaire pour le robot mobile.

Semaines supplémentaires

Semaine du 24/04

Nous avons rencontré de nombreuses difficultés afin de réaliser un script Matlab dans lequel nous chargeons un de nos modèles obtenues et dans lequel on donne la même commande au robot qu'au modèle. Nous avons rencontré aussi des problèmes avec le matériel car des librairies Matlab n’étaient pas présentes sur les ordinateurs utilisés.

Semaine du 02/05

Nous avons enfin réussi à faire un script afin de pouvoir réaliser la validation en ligne d'un modèle. Nous avons pu tester la validation en ligne pour le modèle sur l'axe lacet. Nous remarquons que le comportement estimé et le comportement réel sont très similaires, notre modèle a donc été validé en ligne.

Nous avons voulu réaliser ce test dans l'arène pour l'impact que la force de contact robot/sol aurait sur la figure obtenue. Étonnamment, le comportement estimé et le comportement réel sont similaires. Cela veut dire le modèle que nous avons obtenu de base hors-ligne et avec une campagne d'acquisitions en roues libres, réagit à l'environnement dans lequel on le met.

Pour la fin de notre projet, nous allons essayer d'ajouter des observateurs à nos modèles obtenues et des les valider de nouveau en ligne. Avec l'ajout d'un observateur, les courbes du comportement estimé par le modèle et celle du comportement réel devraient être pratiquement les mêmes et cela devraient être le cas peut importe le temps de la campagne d'acquisitions.

Là on remarque que l'observateur arrive à estimer l'écart entre la position des roues estimée et le modèle, et il fait en sort de compenser l'écart. On arrive à peine à voir notre modèle qui est en bleu sur le graphe, car l'ajout de l'observateur en vert colle parfaitement avec lui, tandis que le comportement estimé des roues en rouge n'atteint pas le modèle. C'est pourquoi un observateur est très important lorsqu'on arrive pas à mesurer ou avoir un impact direct sur l'écart.

Conclusion

Pour ce qui est du cahier des charges, nous avons bien pu accomplir les buts de ce projet et les tâches à réaliser à savoir : L'estimation d'un modèle mathématique du robot mobile, la détermination du modèle à partir des mesures recueillies par le robot, la validation du modèle avec d'autres mesures qui n'ont pas servies à déterminer celui-ci et le test en ligne du modèle. Si le temps nous l'avait permis, nous nous serions lancé à présent à l'identification d'un modèle non linéaire du robot mobile.

Fichiers Rendus

Fichier:Rapport P47.pdf