Implantation d'un filtre FIR-FX-LMS sur FPGA pour l'annulation de Bruit Acoustique
Sommaire
- 1 Cahier des Charges
- 2 Etapes du Projet
- 3 Tableau de bord
- 4 Sources, Tuto & Datasheet
Cahier des Charges
Présentation générale du projet
Contexte
Les problèmes de bruit acoustiques sont de plus en plus présents en industrie avec de plus en plus de moteurs, de transformateurs, de compresseurs, de ventilateur, etc… La plus part du temps, on utilise des moyens passifs pour réduire le bruit, comme des murs, des enclos, des silencieux… Ces systèmes passifs sont utilisés pour leur forte atténuation de bruit sur une large gamme de fréquence. Cependant, ils sont relativement imposants, coûteux et inefficace dans les basses fréquences.
L'utilisation d'un filtre actif permet de résoudre ces problèmes. En effet, grâce au système de Contrôle Actif du bruit (Active Noise Control – ANC), on peut annuler les bruits primaires en superposant un signal inverse à ce bruit primaire. Ce signal inverse possède la même amplitude avec une opposition de phase. La conception d’un ANC est rapide et efficace, il suffit d’un micro pour recueillir le bruit primaire et d’un haut-parleur pour envoyer l’inverse de ce bruit.
Description du projet
On propose ici de réaliser un filtre actif (ANC) permettant d'annuler une source de bruit. Pour cela, nous utiliserons un filtre numérique de type FIR (Finite Impulse Response) avec une adaptation des coefficients par l'algorithme Filtered X Least Mean Square (FX-LMS). Ce filtre sera implémenté sur FPGA permettant de traiter les données en temps réel.
Objectif
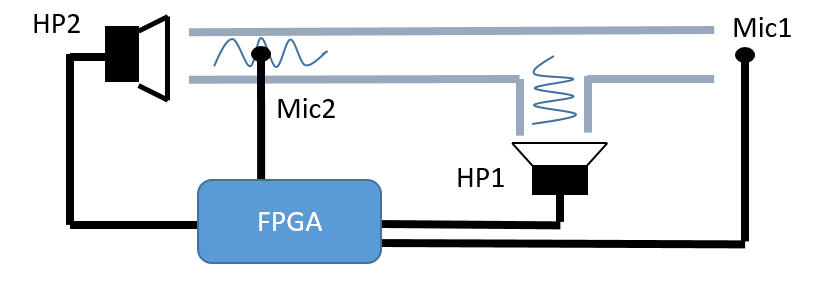
Notre objectif est d'annuler un bruit primaire envoyé par un Haut-parleur grâce à un second Haut parleur :
Le Haut-parleur 2 envoi un bruit primaire qui sera déformé par le tube. Le Haut-parleur 1 devra donc envoyé l'inverse du son du Haut-parleur 2 déformé. Le micro 2 permet de récupérer le bruit primaire et le micro 1 permet de récupéré le son déformé moins le son inverse, c'est à dire à notre erreur de notre filtre.
Le son réceptionné par les micros devra être échantillonné à une fréquence de 48kHz, ainsi une grande partie de l'information sera récupéré et le traitement des signaux aura le temps de s'effectuer.
Nous devrons pouvoir modifier le pas de convergence à distance à l'aide d'une communication filaire, soit à l'aide du protocole SPI, I2C ou UART, nous verrons cela en fonction du matériel disponible. L'envoi des données se fera via mathlab. De plus le FPGA devra envoyer les valeurs des coefficients du filtre que nous afficherons sur mathlab.
Etapes du Projet
Choix techniques : matériel, logiciels, sources
- Board Basys3 contenant un FPGA Artix7 xc7a35t cpg236 -1
- 2 Convertisseur Analogique to Digital : PmodAD2
- 1 Convertisseur Digital to Analogique : PmodDA4
- 2 Haut Parleurs AD2071Z (8ohm/64mm de diamètre)
- 2 microphones
- Matlab
- Vivado 2015.4 Xilinx
Plan de Travail
| Semaine | du 11/01 au 17/01 | du 18/01 au 24/01 | du 25/01 au 31/01 | du 1/02 au 7/02 | du 8/02 au 14/02 | du 15/02 au 21/02 | du 22/02 au 25/02 |
|---|---|---|---|---|---|---|---|
| Réalisation | Etude bibliographique et théorique du Filtre FIR avec l'adaptation par FX-LMS | Simulation des algorithmes sous Matlab | Codage du programme en VHDL et test sur le FPGA Artix7 | Implémentation du code sur Artix7 avec essai pratique | Implémentation du code sur Artix7 avec essai pratique | Développement de la partie communication avec une IHM | Rédaction du rapport de projet |
Tableau de bord
Semaine 1 : du 11/01 au 17/01
Etude théorique du filtre FIR avec adaptation par l'algorithme FX-LMS
1) Le filtre FIR
Un filtre FIR (Finite Impulse Response) est un filtre numérique qui est caractérisé par une réponse basée sur un nombre fini de valeurs du signal d’entrées. Un filtre FIR est décrit par une somme de coefficient multiplié par les valeurs d’entrées.
Si 〖x[i]〗_(1≤i≤n) représente les valeurs du signal d'entrée, bk les valeurs des coefficients et 〖y[i]〗_(1≤i≤n) les valeurs du signal de sortie pour n échantillons, alors un filtre FIR se défit par la combinaison linéaire :
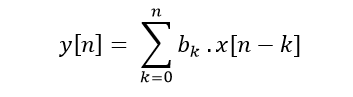
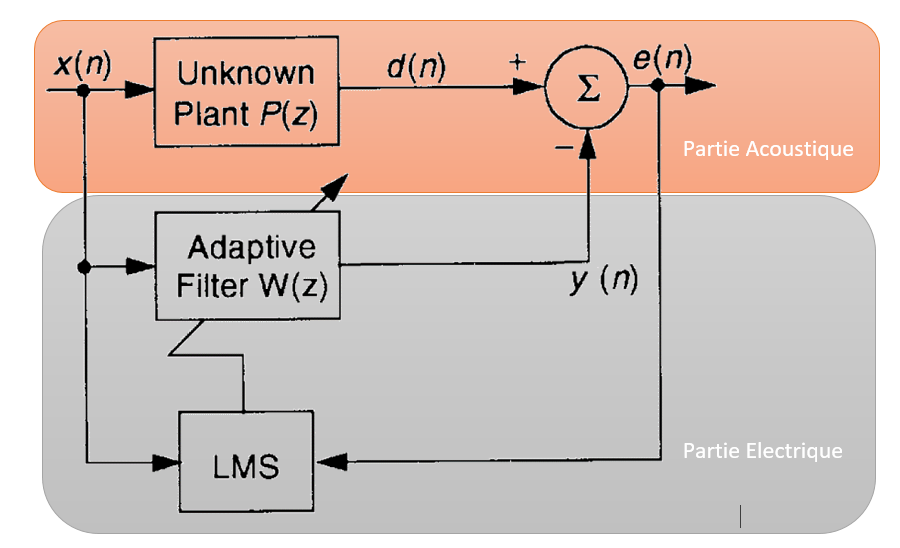
2) Algorithme d'adaptation LMS (Least MeanSqare)
Nous allons utiliser un algorithme adaptatif de type LMS (Least MeanSqare). Cet algorithme est le plus utilisé dans le milieu de l’industrie en raison de sa simplicité. Cet algorithme est une approximation de l’algorithme du gradient déterministe. Le principe de cet algorithme est de trouver les coefficients optimums permettant de décrire le système à modéliser. Il commence par mettre tous les coefficients à zéro puis à chaque étape, calcule les nouveaux coefficients en fonction de l’erreur. Si l’erreur est nulle, alors les coefficients modélisent le système. Voici les équations de cet algorithme :
y(n)=w^T (n)×x(n)
e(n)=d(n)-y(n)
w(n+1)=w(n)+ μ×x(n)×e(n)
Avec :
y : signal de sortie du filtre
x : signal d’entrée du filtre
w : les coefficients du filtre
e : l’erreur récupérée
d : le signal désiré
µ : pas d’adaptation de l’algorithme
Cet algorithme est très efficace mais ne nous permet pas de modéliser correctement notre système
3) Algorithme d'adaptation FX-LMS
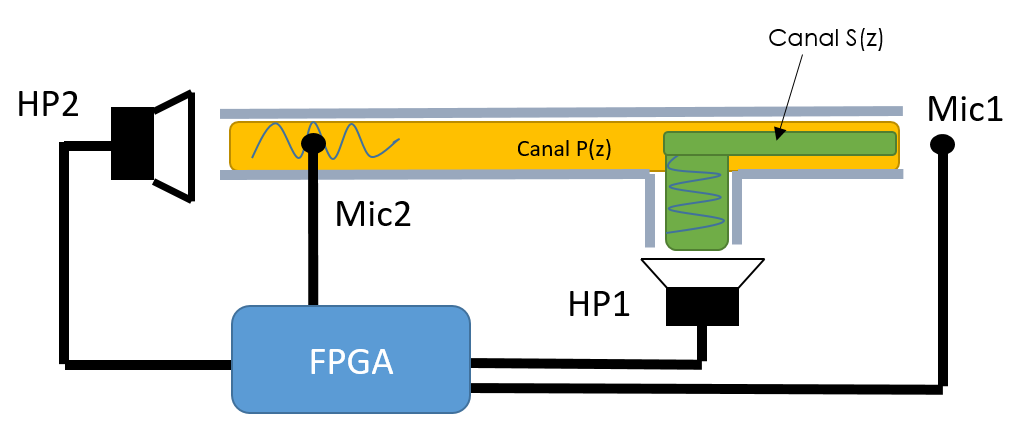
Reprenons notre système :
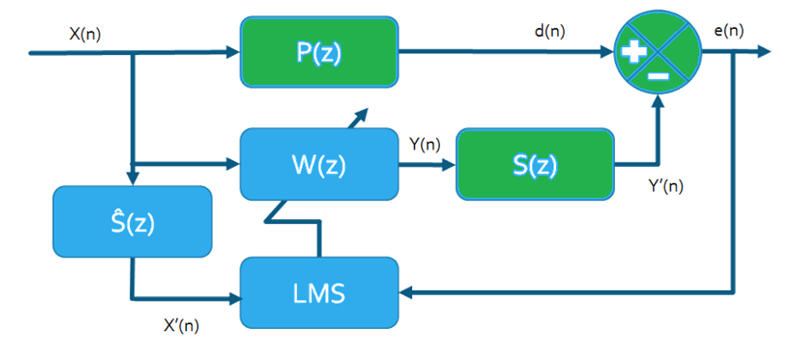
Sur ce schéma, on retrouve deux canaux de propagation du son. Or l'algorithme LMS ne prend en compte un seul canal de propagation. Nous allons donc utiliser l’algorithme FX-LMS. L’introduction du nouveau canal dans notre algorithme peut être traitée de plusieurs manières. Dans notre cas, nous allons procéder en deux : une estimation du canal S puis une modélisation du canal P. Cette méthode engendre une hypothèse : Le canal S est considéré comme stable et ne change jamais Du coup, on pourra modéliser le canal S avec un premier filtre FIR-LMS en mode identification de système puis on utilisera un filtre FIR-FX-LMS en mode modélisation inverse.
La partie verte correspond au domaine acoustique et la partie bleue correspond au domaine électronique, c’est le système que l’on va implanter dans notre FPGA. Le bloc Ŝ(z) correspond à notre canal de propagation S(z) estimé. L’ajout de ce bloc entraine donc une modification de l’équation de l’algorithme :
d(n)=X(n)×P(z)
e(n)=d(n)-S(z)×W(n)×X(n)
W(n+1)=W(n)+ μ ×e(n)×X'(n)
X'(n)= Ŝ(z)×X(n)
Il va à présent nous falloir décrire ces équations dans notre FPGA.
Semaine 2 : du 18/01 au 24/01
Simulation du filtre sous Matlab
Pour simuler notre filtre, nous allons coder les équations de notre filtre dans Matlab en appliquant des signaux théoriques. Le code va se décomposer en deux parties : la première partie permettra de simuler notre filtre en virgule flottante, c’est-à-dire de garder une précisions maximales sur les chiffres puis la deuxième partie sera de simuler cette fois ci en virgule fixe, cela nous permet d’arrondir nos chiffres en fonction d’un nombre de bit prédéfini. La simulation en virgule fixe nous permet de simuler notre schéma électrique, cela dans le but de générer des fichiers de résultats que nous pourrons comparer avec notre code VHDL grâce à un transfert de fichier.
1) Simulation en virgule flotante
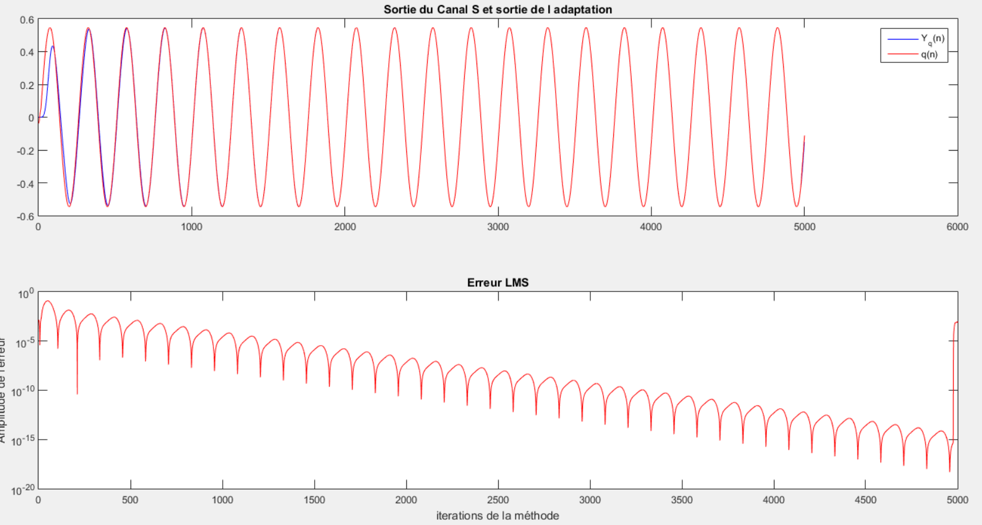
Pour simuler notre système, nous allons utiliser des signaux sinusoïdaux. Les canaux de propagation seront modéliser par des tableaux de coefficients générés aléatoirement par Matlab. Nous allons donc faire passer nos signaux d'entrés dans les canaux de propagation grâce à un produit de convolution puis ensuite nous allons utiliser notre algorithme pour modéliser notre système. Voici les résultats des Simulations :
Sur le premier graphique, on retrouve le signal déformé par le canal en rouge et le signal multiplier par les coefficients modélisé en bleue. Sur le deuxième graphique, on retrouve l’erreur entre le signal modélisé et le signal déformé.
On remarque bien la convergence entre notre signal modélisé et notre signal réel ainsi que la valeur extrêmement faible de notre erreur.
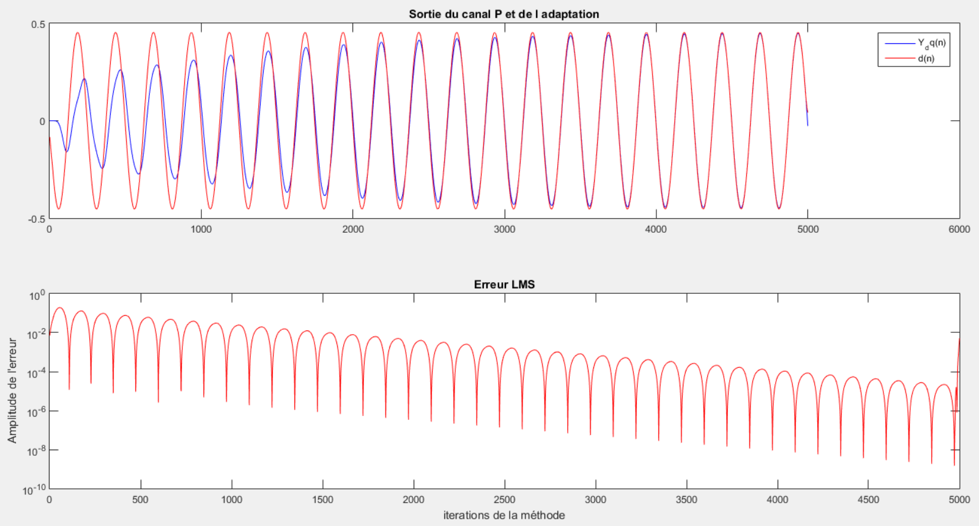
Maintenant que la modélisation de notre canal S est validée, nous pouvons utiliser l’algorithme du FX-LMS, voici le résultat :
Sur le premier graphique, le signal rouge correspond à notre signal déformé par le canal P et le signal bleu le signal envoyé à notre haut-parleur1. Sur le deuxième graphique, on retrouve notre erreur entre les deux signaux.
2) Simulation en virgule flotante
Le but de cette simulation est de se placer en situation réelle, c’est-à-dire de simuler le même comportement que ce qu’il va se passer dans notre FPGA. Pour cela, nous allons fixer chaque valeur sur 16 bits. Cela nous permet de traiter les valeurs avec la même précision que notre FPGA.
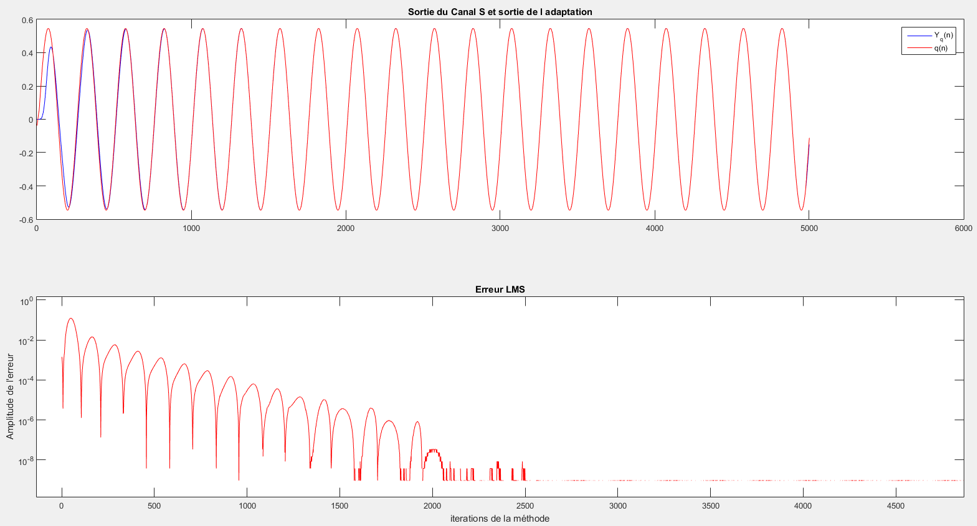
De même que précédemment, voici les résultats de la modélisation du canal S :
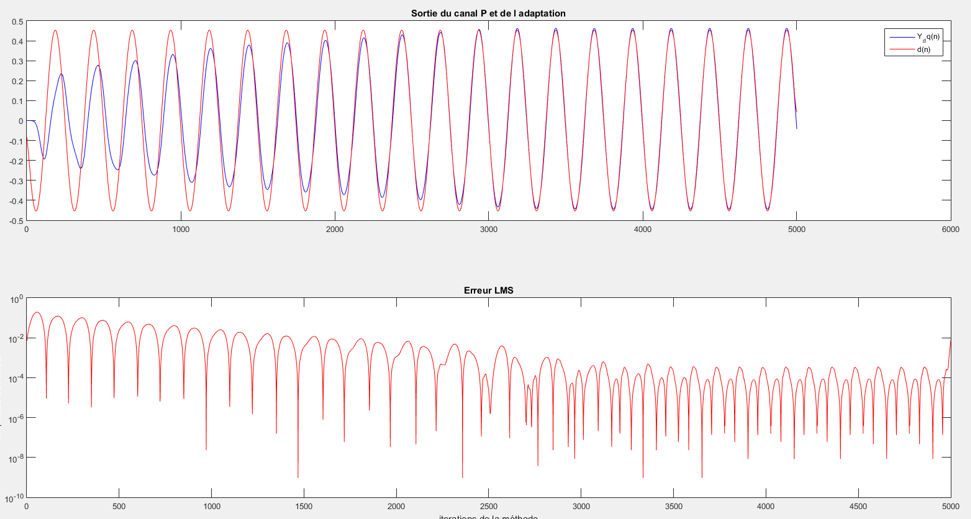
Et le résultat de simulation de l'algorithme total :
Semaine 3 : du 25/01 au 31/01
- Prise de connaissance avec la board Basys3 et son FPGA Artix 7 sur le logiciel Vivado. Nous avons récupéré une IP pour le protocole SPI afin de communiquer avec le DAC.
-Protocole Serial Peripheral Interface (SPI)
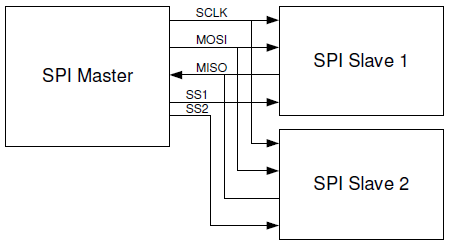
Le SPI est une interface série permettant d'interconnecter les composantes d'un système périphérique avec une minimum de fils. Sur le bus, il y a un maître qui initie toutes les communications et plusieurs esclaves qui transmette des données uniquement lorsque le maître les actives. Le principale avantage de ce protocole est qu'il est en full-duplex, le maître et l'esclave peuvent communiquer simultanément dans les deux sens.
Le bus est composé de quatre fils:
"sclk" pour l'horloge du bus
"mosi" pour les données du maître vers l'esclave
"miso" pour véhiculer les données de l'esclave au maître
"ss" pour activer l'esclave voulu.
-Transfert SPI et communication avec le convertisseur PMOD DA4
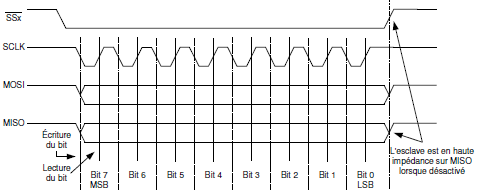
Afin de communiquer avec le PMOD DA4, le maître (le fpga) active la ligne SS de l'esclave (le PMOD) avec lequel il veut parler puis génère le signal d'horloge pour 32 bits. La polarité et la phase du signal sont tel que les données sont lues dès le premier front descendant de l'horloge avec une fréquence de 50MHz (clock du fpga divisé par deux).
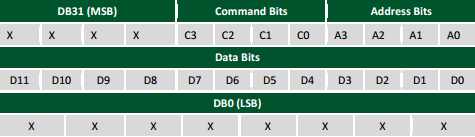
Avant de pouvoir convertir les données il faut initialiser le PMOD en lui envoyant une série de commande. C'est pour cela qu'il y a 32 bits d'informations à envoyé: 4 bits sont dédiés aux commandes, 4 bits pour les adresses des DACs à sélectionner puis 12 bits pour les données à convertir. La première commande envoyé sélectionne la référence interne du PMOD (qui est à 2.5V), la deuxième allume les 8 DACs disponible sur le PMOD puis enfin nous pouvons envoyer les données en continue avec une troisième commande qui écrira et mettra à jours les DACs.
Voici la simulation sur vivado de l'envoie de la donnée "aa" (en hexadécimal) avec ce protocole:
Sur le fil MOSI nous pouvons remarquer que cette série de bits a été envoyé: xxxx 0011 1111 Data xxxx xxxx avec Data = aah
Avec pour commande : "0011" qui demande à écrire et mettre à jours tous les DACs car l'adresse envoyé est "1111".
- Codage du filtre avec adaptation en VHDL :
Nous avons commencé par définir l'architecture de notre composant. Voici cette architecture :
Puis nous avons coder les différents composants que nous avons connecter suivant l'architecture. Il nous a également fallut créer une machine à état permettant de synchroniser les signaux.
Une fois notre Filtre coder, nous avons utilisé un transfert de fichier entre Matlab et Modelsim (Logiciel de simulation de circuit VHDL) pour comparer les résultats :
Nous voyons donc que les courbes ne correspondent pas... Cependant, on remarque que le filtre en VHDL s'adapte par rapport à un signal mais pas par rapport au bon. Cela vient peut-être de la méthode utilisé. C'est à dire que l'erreur de notre filtre est généré par Matlab or Modelsim enregistre normalement une autre erreur. Nous allons donc passer à l'implémentation du Filtre dans le FPGA pour voir si l'erreur vient de la méthode utilisé ou de notre code.
Semaine 3 : du 01/02 au 7/02
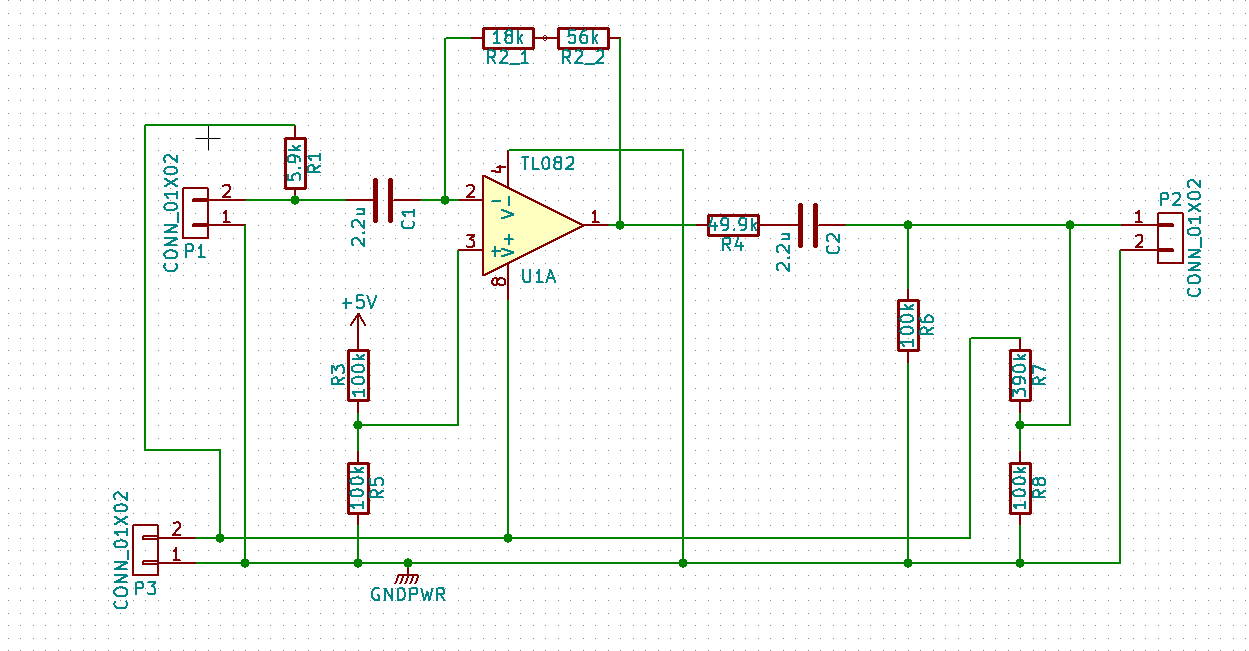
- Création de l'amplificateur pour le micro :
Nous utilisons un microphone electret, nous avons donc besoin d'un circuit permettant l'utilisation du micro. Voici son schéma que nous allons réaliser :
- Création du tube pour notre expérience
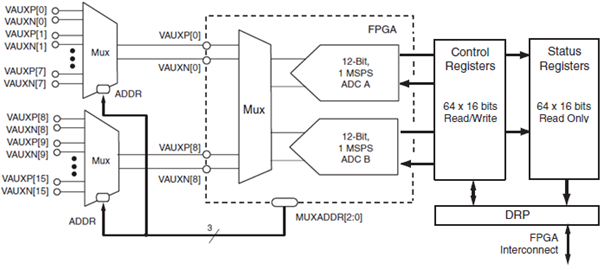
Utilisation du XADC sur la carte Basys3
Nous avons décidé d'utiliser le bloc XADC qui se trouve sur la carte Basys3 plutôt que d'utiliser le PMOD AD2. Ceci nous permet d'aller plus vite dans la conversion du signal (qui est à 100MHz avec le XADC) car nous ne perdons moins de temps avec la communication entre les composants (pas de protocole I2C à utiliser).
Le bloc XADC contient deux ADCs de 12bits à 1 MSPS (Mega Sample Per Seconde) que nous pouvons utiliser simultanément, nous les utiliserons donc pour pouvoir convertir les signaux reçu des deux micros. Cependant, les données convertis par les ADCs sont stockés dans des registres auxquels on accèdes via un DRP (Dynamic Reconfiguration Port) où il est possible de lire un seul registre à la fois. Le signal analogique à convertir doit se trouver entre 0 et 1V, les datas en sortie de l'XADC iront de 000h à FFFh. En sachant que 1 LSB = 1V / 4096, la précision sera de 244µV par bit.
Semaine 4 : du 08/02 au 14/02
Implémentation du son connu sur un bloc RAM du FPGA:
A l'aide du logiciel Matlab, nous avons généré un fichier ".coe" dans lequel se trouve 48000 mots de 16 bits qui représente une sinusoïde avec une fréquence qui augmente par échelon. Lors de l’exécution du processus, les données de la RAM sont lu à une fréquence de 48kHz, ainsi lorsqu'elles sont transféré vers le DAC le son est audible et assez long pour différencier les différentes gammes de fréquences.
Semaine 5 : du 16/02 au 21/02
Test séparé des différents modules:
Test ADC/DAC
Test BRAM
Semaine 6 : du 22/02 au 27/02
Nous avons passé le début de semaine à construire la maquette et à effectuer les premiers tests :
ERRATUM
Après vérification des comparaison entre modelsim et matlab, nous avons remarqué que nous ne faisions pas les bonnes comparaisons. Nous comparions le signal déformé par le canal de propagation S et le signal non déformé. Après correction, voici les résultats :
Finalement, le code VHDL de notre filtre est fonctionnel et devrais fonctionner. Suite au premier test, nous avons des problèmes de calibrage des modules de conversion analogique numérique que nous allons essayer de résoudre.
Sources, Tuto & Datasheet
Liens Basys3: [1]
Comment programmer un Basys3 [2]
Basys3: Référence [3] Schematic [4]
PmodDA4: Datasheet du AD5628 [5] Référence [6] Schematic [7]
PmodAD2: Référence [8] Schematic [9]
IP(Intellectual Property) VHDL pour protocole SPI: [10]
Datasheet Memory ressources [11]